20 Distribution

20.1 Normal distribution

คือ ลักษณะการกระจายตัวของข้อมูลที่เป็นรูประฆังคว่ำ ซึ่งพบมากสุดในธรรมชาติ

\[ f(x) = \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2}(\frac{x-\mu}{\sigma})^{2}} \]

\(Z\)-distribution = Standard normal distribution ของประชากร ที่มี \(\mu = 0\), \(\sigma = 1\)

สามารถสร้าง \(Z\) score ได้จาก

\[ Z = \frac{x-\mu}{\sigma} \]

ค่าของ \(Z\)-score ที่พบบ่อย

\(Z\)-score	\(p\)-value (one-tailed)	Confidence interval
<-1.65, >1.65	0.10	90%
<-1.96, >1.96	0.05	95%
<-2.58, >2.58	0.01	99%

20.2 \(t\)-distribution

คือ การกระจายตัวของอัตราส่วนของความต่างของค่าเฉลี่ยระหว่างกลุ่มตัวอย่างกับความผิดพลาดของการวัดที่สุ่มจากประชากร ใช้ใน t-test

\[ f(t) = \frac{\Gamma(\frac{v+1}{2})}{\sqrt{v\pi}\Gamma(\frac{v}{2})}(1+\frac{t^{2}}{v})^{-\frac{v+1}{2}} \]

t_dist <- data.frame(x = x, 
                        `DF 1` = dt(x, df = 1),
                        `DF 2` = dt(x, df = 2),
                        `DF 4` = dt(x, df = 4),
                        `DF 8` = dt(x, df = 8)) |> 
  pivot_longer(-x,names_to = "Param", values_to  = "T.distribution" ) 

ggplot(t_dist, aes(x = x, y = T.distribution, col = Param)) + 
  geom_line(alpha = 0.8, linewidth = 0.5) +
  xlim(-4,4) +
  labs(title = "t-distribution", x = "Values", y = "Rate")

สามารถสร้าง \(t\)-score (\(t\) -value) ได้จาก

\[ t = \frac{\bar{x}-\mu}{SE} = \frac{\bar{x}-\mu}{s/\sqrt{n}} \]

Note: \(t\)-score บางครั้งเป็นคำศัพท์เฉพาะทาง

Education assessment \(\mu = 50\), \(\sigma = 10\)
Bone density เทียบกับผู้ป่วยอายุ 30 ปี \(\mu = 0\), \(\sigma = 1\)

20.3 Uniform distribution

คือ การกระจายตัวของข้อมูลที่อัตราการเกิดเท่าๆ กัน เช่น ทอยลูกเต๋าไม่ถ่วงน้ำหนัก 1 ลูก ดึงไพ่จากสำรับ เป็นต้น

\[ f(x) = \begin{cases} \frac{1}{b-a} \ \text{for} \ a \leq x \leq b \\ 0 \ \text{for} \ x<a \ \text{or} \ x>b \end{cases} \]

x <- seq(0,10,1)

unif_dist <- data.frame(x = x, 
                     dice = dunif(x, min = 1 ,max = 6)) |> 
  pivot_longer(-x,names_to = "Param", values_to  = "Uniform.distribution" ) 

ggplot(unif_dist, aes(x = x, y = Uniform.distribution)) + 
  geom_point() +
  geom_segment(col = "darkblue", xend = x, yend = 0) +
  scale_x_continuous(breaks = 0:10, limits = c(0,10)) +
  labs(title = "Dice rolls", x = "Face", y = "Rate")

20.4 Binomial distribution

คือ การกระจายตัวของโอกาสสำเร็จในการทดลองที่มีผลลัพธ์สองรูปแบบ เช่น หัว/ก้อย ชนะ/แพ้

\[ f(x,n,p) = P(X = x) = {n\choose x}p^{x}(1-p)^{n-k} \]

# 20 trials, prob of success = 10% to 90%
binom_dist <- map_dfc(c(0.1, 0.3, 0.5, 0.7, 0.9), ~dbinom(1:20, 20, .x)) |> 
  set_names(paste0("Prob = ", c(0.1, 0.3, 0.5, 0.7, 0.9) )) |> 
  mutate(numb_success = 1:20) |> 
  pivot_longer(!numb_success, names_to = "Prob", values_to = "rate") 

ggplot(binom_dist, aes(x = numb_success, y = rate, col = Prob)) + 
  geom_point(size = 0.8) +
  geom_line() +
  scale_x_continuous(breaks = seq(0,21,1), limits = c(0,21)) +
  labs(x = "Number of success", y = "Rate")

20.5 Negative binomial distribution

คือ การกระจายของจำนวนครั้งที่ไม่สำเร็จก่อนที่จะได้จำนวนครั้งของการสำเร็จที่ต้องการ

\[ p(k) = {r-1+k \choose r-1}p^{r-1}(1-p)^{k}p = {r-1+k \choose k}p^{r}(1-p)^{k} \]

nbprob_dist <- map_dfc(c(0.1, 0.3, 0.5, 0.7, 0.9), \(x) dnbinom(1:20, 20,x)) |> 
  set_names(paste0("Prob = ", c(0.1, 0.3,0.5,0.7,0.9) )) |> 
  mutate(numb_failure = 1:20) |> 
  pivot_longer(!numb_failure, names_to = "Prob", values_to = "rate") 

ggplot(nbprob_dist, aes(x = numb_failure, y = rate, col = Prob)) + 
  geom_point(alpha = 0.9, size =2) +
  geom_line() +
  scale_x_continuous(breaks = seq(0,20,2)) +
  theme_bw() +
  labs(x = "Number of failures", y = "Rate")

20.6 Hypergeometric distribution

คือ การกระจายตัวของโอกาสที่จะสุ่มได้เป้าหมายที่ต้องการจากการหยิบสุ่มแบบใส่คืน (Sampling with replacement) ใช้ใน Fisher’s exact test

\[ f(x,n,M,N) = p(X=x) = \frac{{M \choose x}{N-M \choose n-x}}{N \choose n} \]

hyper_dist <- map_dfc(c(10,20,30), ~dhyper(1:30, .x, 30, 30)) |>  
  set_names(paste0("Black = ", c(10,20,30))) |> 
  mutate(numb_success = 1:30) |> 
  pivot_longer(!numb_success, names_to = "Pop", values_to = "rate") 

ggplot(hyper_dist, aes(x = numb_success, y = rate, col = Pop)) + 
  geom_point(size = 0.8) +
  geom_line() +
  scale_x_continuous(breaks = seq(0,30,2), limits = c(0,30)) +
  labs(title = "Probablity of getting black balls from 30 picks", 
       x = "Number of black balls picked", y = "Rate", col = "Total black balls\n in the bag")

20.7 Poisson distribution

คือ การกระจายตัวของโอกาสที่จะเกิดเหตุการณ์เท่ากับจำนวนครั้งที่ต้องการภายใต้ช่วงเวลาใดเวลาหนึ่ง

\[ f(k) = P(X = k) = \frac{\lambda^{k}}{k!}e^{-\lambda} \]

\[ \lambda = \frac{k}{t} \]

pois_dist <- map_dfc(c(1, 2, 4, 10), ~dpois(1:20, .x)) |>  
  set_names(paste0("Mean = ", c(1, 2, 4, 10))) |> 
  mutate(numb_event = 1:20) |> 
  pivot_longer(!numb_event, names_to = "Mean", values_to = "value") |> 
  mutate(Mean = fct_relevel(Mean, paste0("Mean = ", c(1, 2, 4, 10))))

ggplot(pois_dist, aes(x = numb_event, y = value, col = Mean)) + 
  geom_point(size = 0.8) +
  geom_line() + 
  scale_x_continuous(breaks = seq(0,20,2), limits = c(0,21)) +
  labs(title = "Probablity that certain number of events will occur", 
       x = "Number of events", y = "Rate", col = "Average number of events")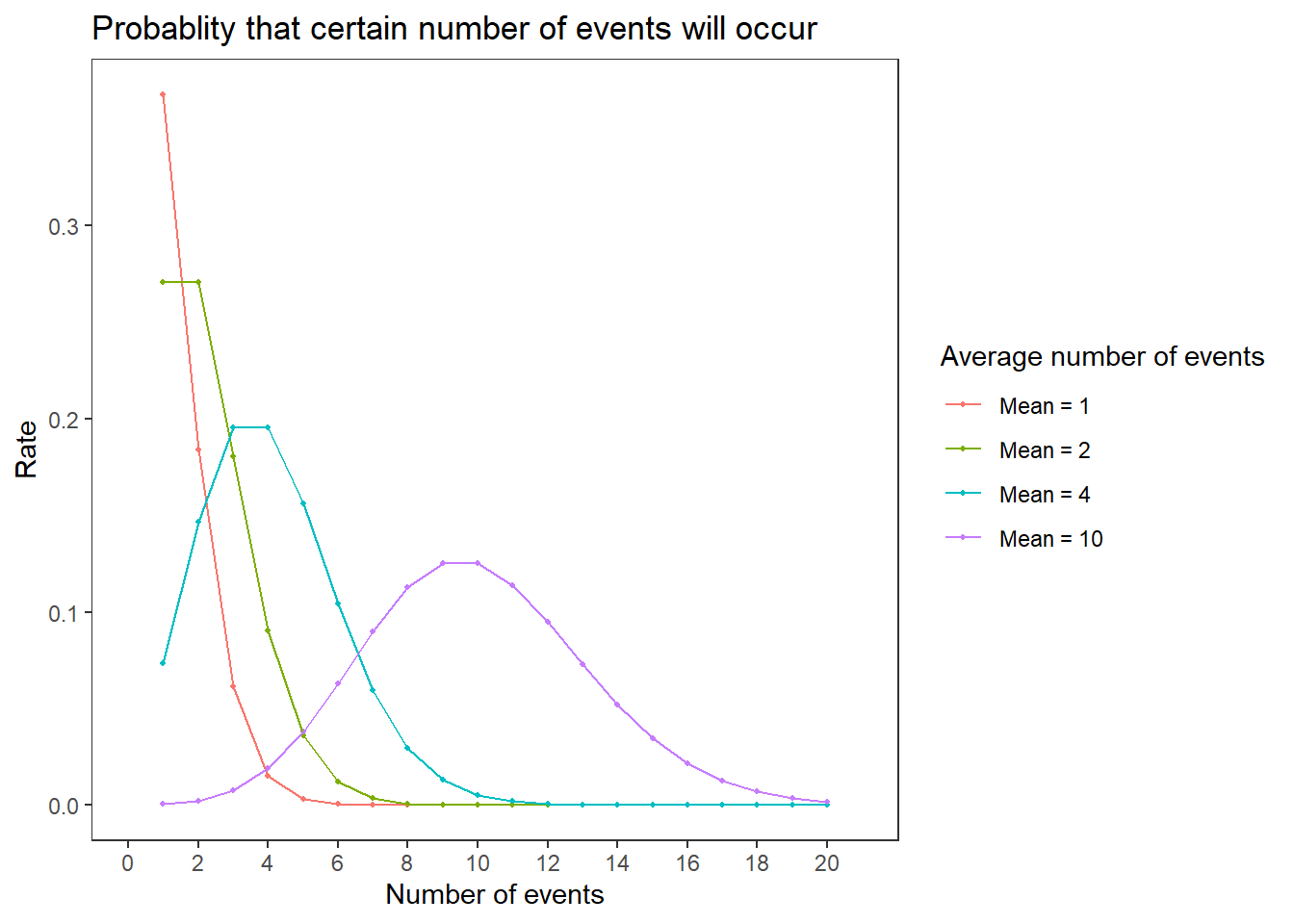

การกระจายตัวแบบ Poisson เป็นการกระจายตัวแบบพื้นฐานในการนับจำนวนต่างๆ รวมถึงจำนวนยีนที่เกิดขึ้นจาก RNA sequencing profile

19 Pathway analysis

21 Session info