15 Principal component analysis

15.1 Principle

Principal component analysis (PCA) คือ วิธีการลดจำนวนมิติของข้อมูล (Dimensional reduction) เพื่อให้ง่ายต่อการวิเคราะห์และสร้างภาพ โดยที่ PCA จะพยายามเก็บข้อมูลที่สำคัญไว้

ยกตัวอย่างเป็นภาพ สมมติท่านต้องการที่จะวิเคราะห์แบ่งลักษณะของรูปจากสีของรูปภาพ แต่เฉดสีนั้นมีมากมาย

ถ้าเป็นข้อมูลอาจจะมีรูปแบบลักษณะนี้

ABCDEFGHIJ0123456789

	Picture_A <dbl>	Picture_B <dbl>	Picture_C <dbl>	Picture_D <dbl>	Picture_E <dbl>	Picture_F <dbl>	Picture_G <dbl>	Picture_H <dbl>	Picture_I <dbl>
PaleRed	-2.0686670	7.253815	9.49281009	6.338540	8.273959	4.47989502	13.7231198	18.5045004	-0.7646529
LightRed	6.7184877	6.426464	-1.28027292	7.995346	11.823893	6.81820714	2.7494272	12.5447722	-1.8922639
MediumRed	2.6731021	5.704929	9.74354898	10.290517	5.146352	0.11221368	4.8946828	12.6809739	-3.9450925
DarkRed	2.6482741	6.895126	2.03324093	8.305544	9.833314	4.40356867	5.9097090	15.8288828	-4.1388629
VerydarkRed	3.5492478	6.878133	1.12719809	6.022205	11.558222	2.47560502	2.5486581	6.1186805	-1.2958939
PaleBlue	6.8416646	6.821581	-0.09191291	10.446423	10.903460	-0.14428832	5.5505861	4.9763384	3.4719433
LightBlue	-2.1818119	6.688640	11.59967734	9.980512	10.317029	-0.02933531	5.1068936	6.3246709	5.4393926
MediumBlue	8.0705531	6.553918	-2.33741451	8.645191	8.077882	-0.20307235	3.3538585	12.9577395	3.8303534
DarkBlue	4.5114373	5.938088	4.98348192	7.716195	7.450887	1.93818696	4.1958791	5.4619642	-0.4546292
VerydarkBlue	10.5850097	5.694037	7.93590496	5.116282	6.927614	0.07648883	3.8977982	2.6222831	1.2389997

ซึ่งการที่จะนำข้อมูลสีทุกจุดมาวิเคราะห์นั้น อาจจะต้องใช้เครื่องคอมพิวเตอร์ที่มีสมรรถนะสูงมาก และข้อมูลส่วนใหญ่ก็ไม่ได้ต่างกันมากนัก ท่านจึงตัดสินใจรวมสีที่มีลักษณะใกล้เคียงกันเป็นกลุ่มๆ

จากกระบวนการนี้ รวมสีที่ใกล้กันเป็นกลุ่มเดียว ส่งผลให้เกิดการลดจำนวนมิติของข้อมูลลง โดยที่ยังเหลือข้อมูลที่มีความสำคัญอยู่

ABCDEFGHIJ0123456789

	Picture_A <dbl>	Picture_B <dbl>	Picture_C <dbl>	Picture_D <dbl>	Picture_E <dbl>	Picture_F <dbl>	Picture_G <dbl>	Picture_H <dbl>	Picture_I <dbl>
Red	-2.068667	10.070553	11.294763	4.869978	7.253815	11.769588	6.876891	8.885813	8.274931
Blue	6.718488	6.511437	10.825540	6.355544	6.426464	8.690441	7.597115	8.828518	7.595399
Green	2.673102	12.585010	9.944314	6.874804	5.704929	7.470187	7.533345	14.474409	6.681065
Yellow	2.648274	6.647290	9.215618	1.566533	6.895126	7.097645	8.779965	8.096916	15.449758
Orange	3.549248	5.714639	9.266497	14.188935	6.878133	5.526465	7.916631	15.065882	4.996939

ซึ่ง PCA นั้นทำการลดมิติของข้อมูลลง โดยรวมข้อมูลอื่นๆ เข้าหาข้อมูลที่มีความสำคัญมากที่สุด นั่นคือ ข้อมูลที่มีความแปรปรวนสูงที่สุด ยกตัวอย่างข้อมูลสองมิติชุดหนึ่ง

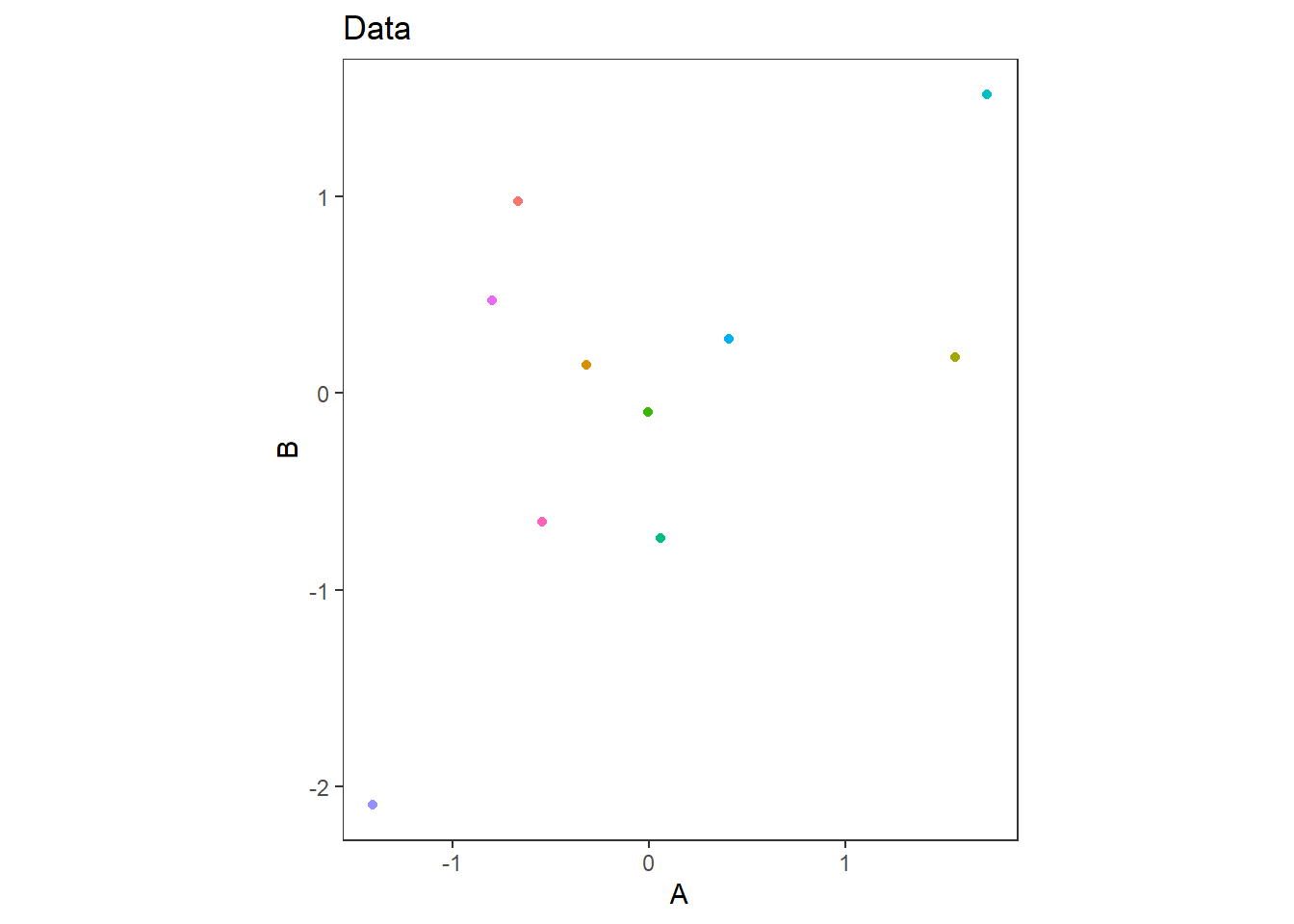
ในการวิเคราะห์ PCA ข้อมูลจะถูกลดมิติลงโดยการพยายามดึงเข้าสู่เส้นที่สามารถอธิบายความแปรปรวนได้ดีที่สุด ซึ่งก็คือ Principal component

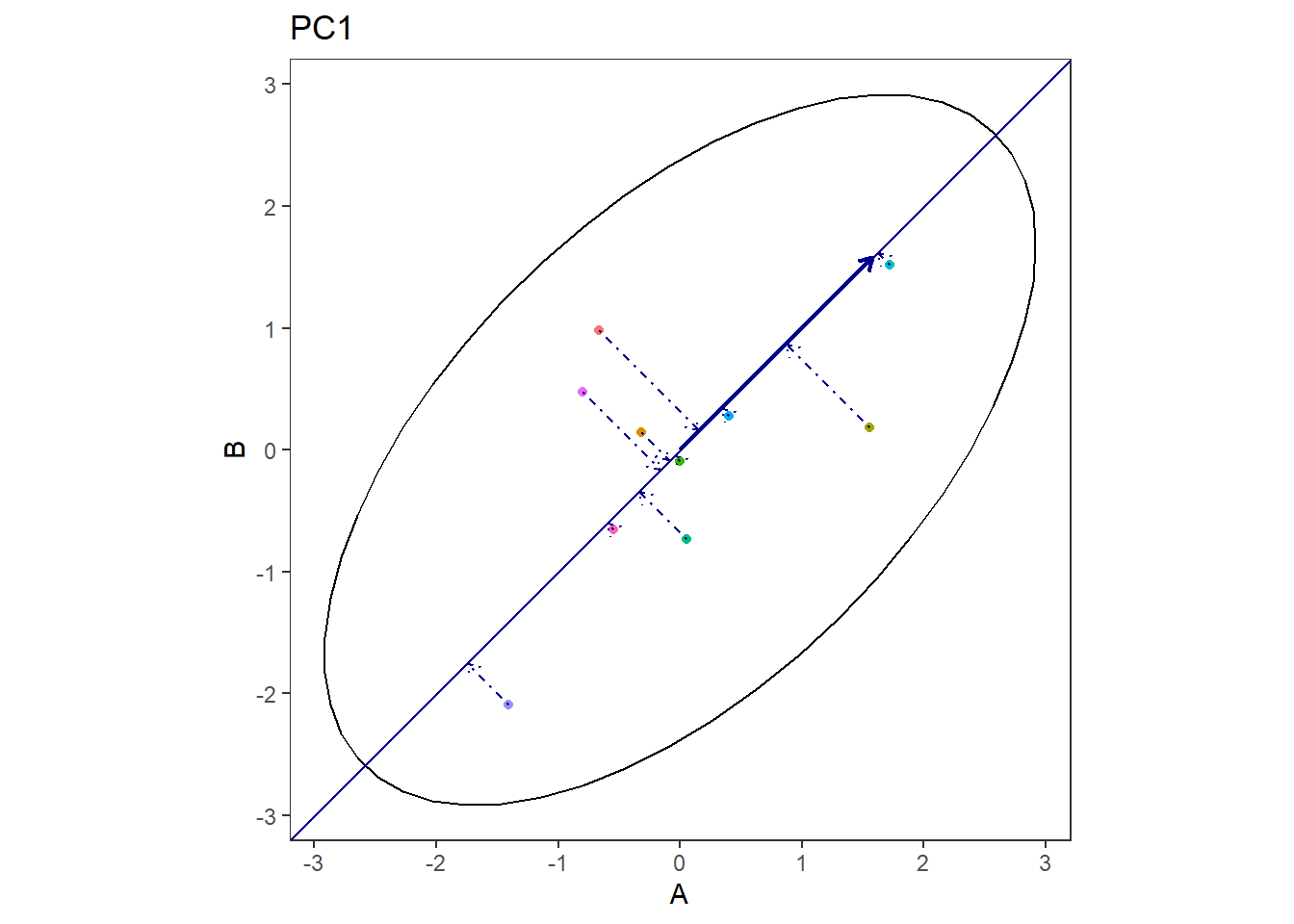
สังเกตว่า เส้นแนวเฉียงนั้น เป็นเส้นที่ข้อมูลแต่ละจุดห่างกันมากที่สุดใน 1 มิติ ซึ่งก็คือเส้นที่สามารถอธิบายความแปรปรวนได้ดีที่สุดนั่นเอง

ส่วนเส้นต่อมาที่ตั้งฉาก คือเส้นที่อธิบายความแปรปรวนได้ดีที่สุดเป็นลำดับสอง

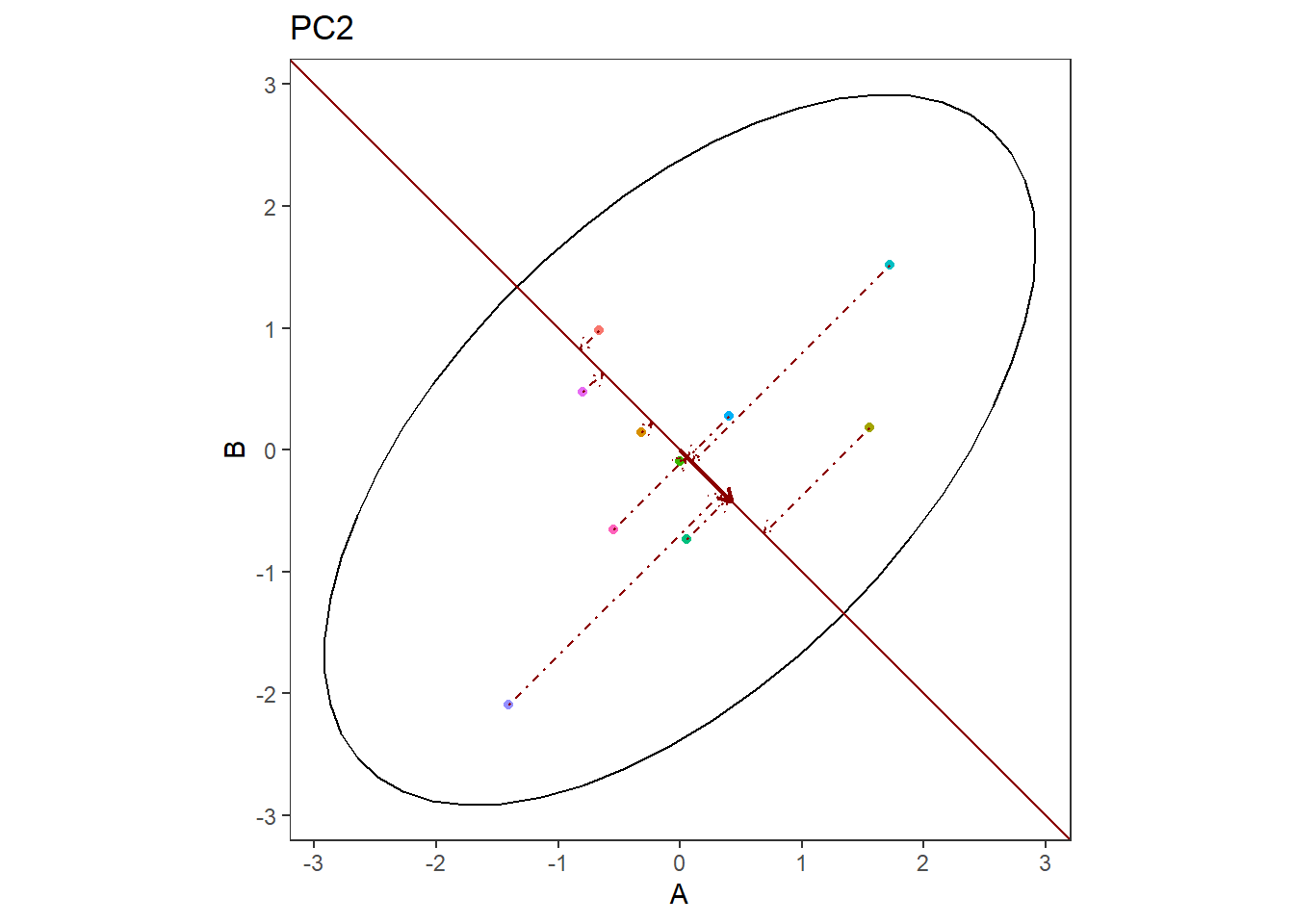
เมื่อนำข้อมูลทั้งหมดมาสร้างเป็นกราฟใหม่ จะได้ข้อมูลที่ยังลงเหลือความแปรปรวนที่มากที่สุดไว้ทั้งสองมิติ

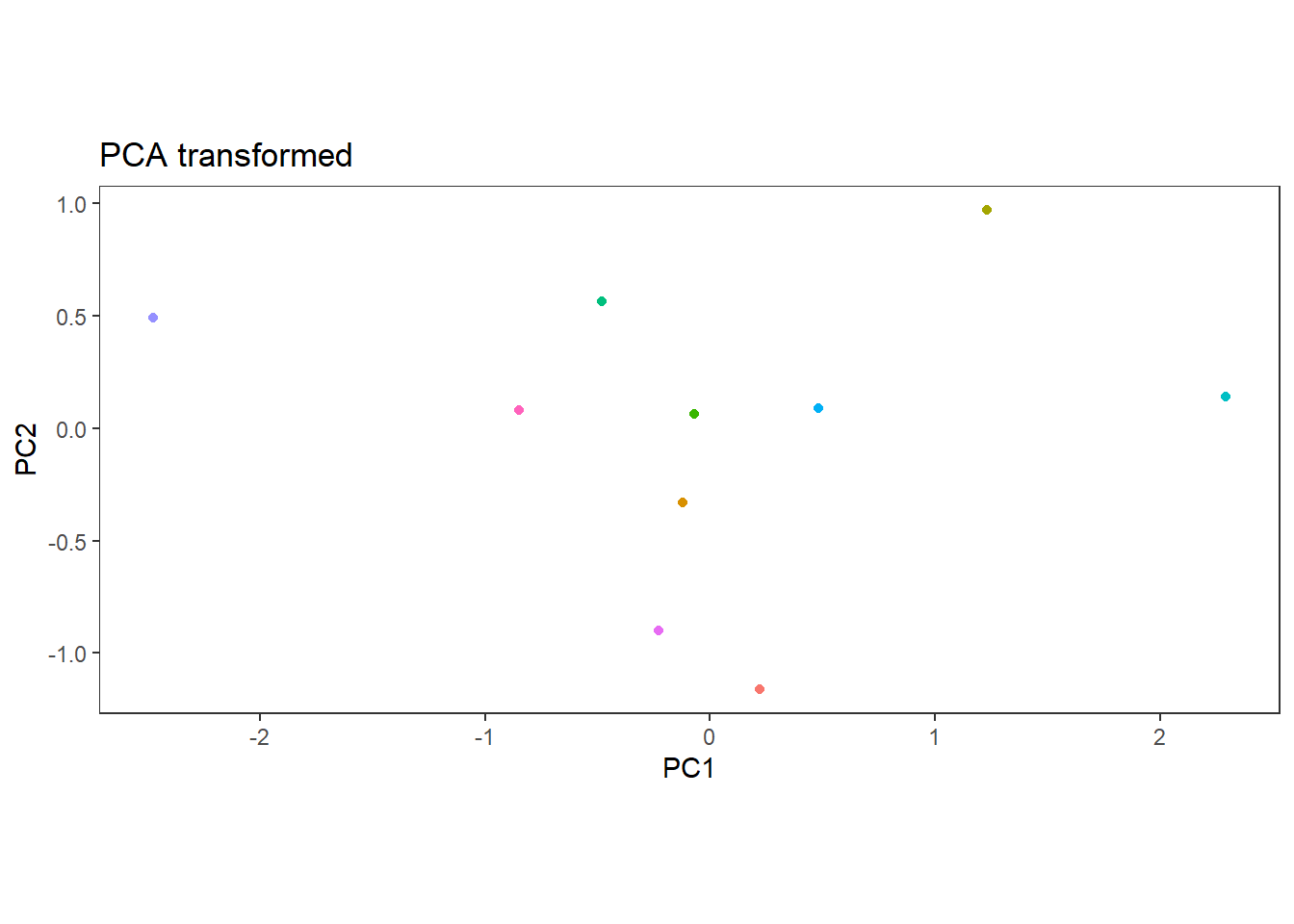
การลดมิติของข้อมูลนี้ อาจจะยังไม่เห็นผลนัก เนื่องจากข้อมูลมีแค่สองมิติเท่านั้น แต่ในสถานการณ์ซึ่งมีข้อมูลสูงมาก โดยเฉพาะเมื่อมี Feature มากกว่า Observations นั้น การลดข้อมูลจะมีประสิทธิภาพมาก โดยเฉพาะข้อมูลประเภท High-throughput (จำนวนยีนมากกว่าตัวอย่าง)

Credit: https://stackoverflow.com/questions/2639430/graphing-perpendicular-offsets-in-a-least-squares-regression-plot-in-r

15.2 Manually calculate PCA

ต่อไปจะแสดงวิธีการคำนวณ PCA เพื่อให้เข้าใจลำดับของการวิเคราะห์

set.seed(123)
data <- matrix(c(
  rnorm(10, mean = 20, sd = 2),
  rnorm(10, mean = 1, sd = 2),
  rnorm(10, mean = 4, sd = 5)),
  ncol = 3
)
colnames(data) <- c("A", "B", "C")
data

##              A           B          C
##  [1,] 18.87905  3.44816359 -1.3391185
##  [2,] 19.53965  1.71962765  2.9101254
##  [3,] 23.11742  1.80154290 -1.1300222
##  [4,] 20.14102  1.22136543  0.3555439
##  [5,] 20.25858 -0.11168227  0.8748037
##  [6,] 23.43013  4.57382627 -4.4334666
##  [7,] 20.92183  1.99570096  8.1889352
##  [8,] 17.46988 -2.93323431  4.7668656
##  [9,] 18.62629  2.40271180 -1.6906847
## [10,] 19.10868  0.05441718 10.2690746

เริ่มต้นด้วยการ Normalize ข้อมูลให้อยู่ในรูป Mean-centering

scaled_data <- apply(data,2, \(x) (x-mean(x))/sd(x))
scaled_data

##                  A           B          C
##  [1,] -0.665875352  0.97821584 -0.6910813
##  [2,] -0.319572479  0.14564661  0.2219402
##  [3,]  1.555994430  0.18510203 -0.6461534
##  [4,] -0.004316756 -0.09434713 -0.3269546
##  [5,]  0.057310762 -0.73642490 -0.2153829
##  [6,]  1.719927421  1.52040423 -1.3559540
##  [7,]  0.405008410  0.27862049  1.3561812
##  [8,] -1.404601888 -2.09545793  0.6208920
##  [9,] -0.798376211  0.47466195 -0.7666212
## [10,] -0.545498338 -0.65642119  1.8031341

scaled_data <- scale(data, center = TRUE, scale = TRUE) # Same
scaled_data

##                  A           B          C
##  [1,] -0.665875352  0.97821584 -0.6910813
##  [2,] -0.319572479  0.14564661  0.2219402
##  [3,]  1.555994430  0.18510203 -0.6461534
##  [4,] -0.004316756 -0.09434713 -0.3269546
##  [5,]  0.057310762 -0.73642490 -0.2153829
##  [6,]  1.719927421  1.52040423 -1.3559540
##  [7,]  0.405008410  0.27862049  1.3561812
##  [8,] -1.404601888 -2.09545793  0.6208920
##  [9,] -0.798376211  0.47466195 -0.7666212
## [10,] -0.545498338 -0.65642119  1.8031341
## attr(,"scaled:center")
##         A         B         C 
## 20.149251  1.417244  1.877206 
## attr(,"scaled:scale")
##        A        B        C 
## 1.907568 2.076147 4.654046

หลังจากนั้นเราจะทำการคำนวณ Covariance matrix ในที่นี้จะใช้แบบ Pearson’s

Note: ถ้ากลับไปพิจารณาสูตร Covariance Pearson’s แล้ว จะได้ว่า

$cov = \frac{1}{n-1}({A^{T}A})$

โดย $n$ คือ จำนวนแถวของ Matrix $A$

cov_matrix <- t(scaled_data) %*% scaled_data / (nrow(scaled_data) - 1) # matrix multiplication
cov_matrix

##            A          B          C
## A  1.0000000  0.5776151 -0.4059593
## B  0.5776151  1.0000000 -0.5673487
## C -0.4059593 -0.5673487  1.0000000

cov_matrix <- cov(scaled_data)
cov_matrix # same

##            A          B          C
## A  1.0000000  0.5776151 -0.4059593
## B  0.5776151  1.0000000 -0.5673487
## C -0.4059593 -0.5673487  1.0000000

หลังจากนั้นเราทำการแยกทิศทางของความแปรปรวนออกมาโดยวิธี Eigendecomposition ซึ่งสำหรับ PCA แล้ว ซึ่ง Eigenvector นั้นบ่งบอกถึงทิศทางของความแปรปรวนของข้อมูลที่ตั้งฉากกัน โดยมีขนาดของการกระจายตัวของข้อมูล คือ Eigenvalue

eigen_info <- eigen(cov_matrix)
eigen_info

## eigen() decomposition
## $values
## [1] 2.0376621 0.5941719 0.3681659
## 
## $vectors
##            [,1]       [,2]       [,3]
## [1,] -0.5596713 0.69413342 -0.4527105
## [2,] -0.6151534 0.01806984  0.7882003
## [3,]  0.5552966 0.71961954  0.4168854

โดย vectors คือ Eigenvector หรือ ทิศทางของความแปรปรวน (เรียงตามคอลัมน์) ส่วน values คือ Eigenvalues หรือ ขนาดของความแปรปรวน

Note: เราสามารถคำนวณ Eigenvalue และ Eigenvector กลับไปเป็น Covariance matrix

$A = VQV^{-1}$

eigen_back <- 
  eigen_info$vectors %*% diag(eigen_info$values) %*% solve(eigen_info$vectors)

round(sum(eigen_back - cov_matrix), 10) # Diff nearly 0 due to algorithm

## [1] 0

ต่อไปจะต้องเรียง Eigenvector ตามขนาดของ Eigenvalues จากน้อยไปมาก ซึ่งนั้นก็คือ Principal component ของข้อมูล (PC1, PC2, PC3, ….) นั่นหมายความว่า $n_{PC} \leq n_{Obs}$ เสมอ

sorted_eigenvalues <- eigen_info$values
sorted_eigenvectors <- eigen_info$vectors[, order(-sorted_eigenvalues)] # Decreasing order

num_components <- 3  # Adjust this as needed
selected_eigenvectors <- sorted_eigenvectors[, 1:num_components]

สุดท้ายเมื่อทำการคูณข้อมูลเดิมกลับไปด้วย Eigenvectors ที่เรียงแล้ว จะได้ ข้อมูลของความแปรปรวนข้อมูลแต่ละคอลัมน์ในแต่ละ PC

pca_result <- scaled_data %*% selected_eigenvectors
colnames(pca_result) <- paste0("PC", 1:ncol(selected_eigenvectors))
pca_result

##              PC1         PC2        PC3
##  [1,] -0.6128366 -0.94184573  0.7843772
##  [2,]  0.2125032 -0.05948164  0.3519961
##  [3,] -1.3435184  0.61842786 -0.8278895
##  [4,] -0.1211029 -0.23998416 -0.2087128
##  [5,]  0.3013377 -0.12851951 -0.6961855
##  [6,] -2.6508325  0.24556160 -0.1455235
##  [7,]  0.3550169  1.26209896  0.6016293
##  [8,]  2.4199227 -0.56603968 -0.7569218
##  [9,] -0.2708638 -1.09727813  0.4159689
## [10,]  1.7103737  0.90706045  0.4812617

15.3 PCA by R function

ท่านไม่จำเป็นต้องคำนวณ PCA ตามทั้งหมดที่กล่าวมาขั้นต้น เนื่องจาก R ได้มีฟังก์ชันสำหรับวิเคราะห์ PCA ไว้ให้แล้ว ในที่นี้จะลองสร้างสถานการณ์ที่ Features > Observations

set.seed(123)

data <- matrix(
  sapply(1:10, \(x) rnorm(5, mean = sample(1:20, 1), sd = sample(1:10, 1))),
  ncol = 10
)
colnames(data) <- LETTERS[1:10]

as.data.frame(data)

ABCDEFGHIJ0123456789

A <dbl>	B <dbl>	C <dbl>	D <dbl>	E <dbl>	F <dbl>	G <dbl>	H <dbl>	I <dbl>	J <dbl>
18.570620	10.070553	21.652869	2.400106	17.284334	8.769588	0.8768292	-2.594688	15.131765	6.000378
9.931333	6.511437	17.429859	9.402037	9.838178	5.690441	28.3516477	4.144220	-9.390022	3.944274
18.718488	12.585010	9.498826	17.494274	3.344357	4.470187	20.6636960	1.839351	7.676910	3.784626
14.673102	6.647290	2.940560	8.982245	14.056131	4.097645	2.0151313	12.449363	3.990834	7.910586
14.648274	5.714639	3.398471	1.841186	13.903201	2.526465	7.7769213	10.141964	4.727533	8.344629

pc <- prcomp(data, scale. = TRUE, center = TRUE)
str(pc)

## List of 5
##  $ sdev    : num [1:5] 2.03 1.88 1.45 4.94e-01 2.83e-16
##  $ rotation: num [1:10, 1:5] -0.196 -0.424 -0.336 -0.274 0.267 ...
##   ..- attr(*, "dimnames")=List of 2
##   .. ..$ : chr [1:10] "A" "B" "C" "D" ...
##   .. ..$ : chr [1:5] "PC1" "PC2" "PC3" "PC4" ...
##  $ center  : Named num [1:10] 15.31 8.31 10.98 8.02 11.69 ...
##   ..- attr(*, "names")= chr [1:10] "A" "B" "C" "D" ...
##  $ scale   : Named num [1:10] 3.61 2.92 8.36 6.37 5.36 ...
##   ..- attr(*, "names")= chr [1:10] "A" "B" "C" "D" ...
##  $ x       : num [1:5, 1:5] -1.242 -0.599 -2.375 1.895 2.322 ...
##   ..- attr(*, "dimnames")=List of 2
##   .. ..$ : NULL
##   .. ..$ : chr [1:5] "PC1" "PC2" "PC3" "PC4" ...
##  - attr(*, "class")= chr "prcomp"

rotation คือ Eigenvectors ที่คำนวณจาก eigen
sdev คือ รากที่สองของ Eigenvalues ที่คำนวณจาก eigen
x คือ ข้อมูลสุดท้ายที่ถูกลดมิติแล้ว

สังเกตว่าสุดท้าย PC จะไม่เกินจำนวน Observations = 5

pc$x

##             PC1          PC2        PC3          PC4           PC5
## [1,] -1.2422037 -2.971150049 -0.8164442 -0.009920526  3.701466e-16
## [2,] -0.5994732  2.075884300 -1.9908362 -0.039263516  4.440892e-16
## [3,] -2.3753407  0.963616858  1.7962551  0.097225061 -2.220446e-16
## [4,]  1.8951608 -0.003007043  0.6758462 -0.718606015  3.330669e-16
## [5,]  2.3218568 -0.065344065  0.3351791  0.670564995  2.220446e-16

15.3.1 Biplot

คือการพล็อตกราฟเพื่อบ่งบอก ว่า แต่ละ Features ดั้งเดิมนั้น มีผลต่อ PC มากน้อยเพียงใด

biplot(pc)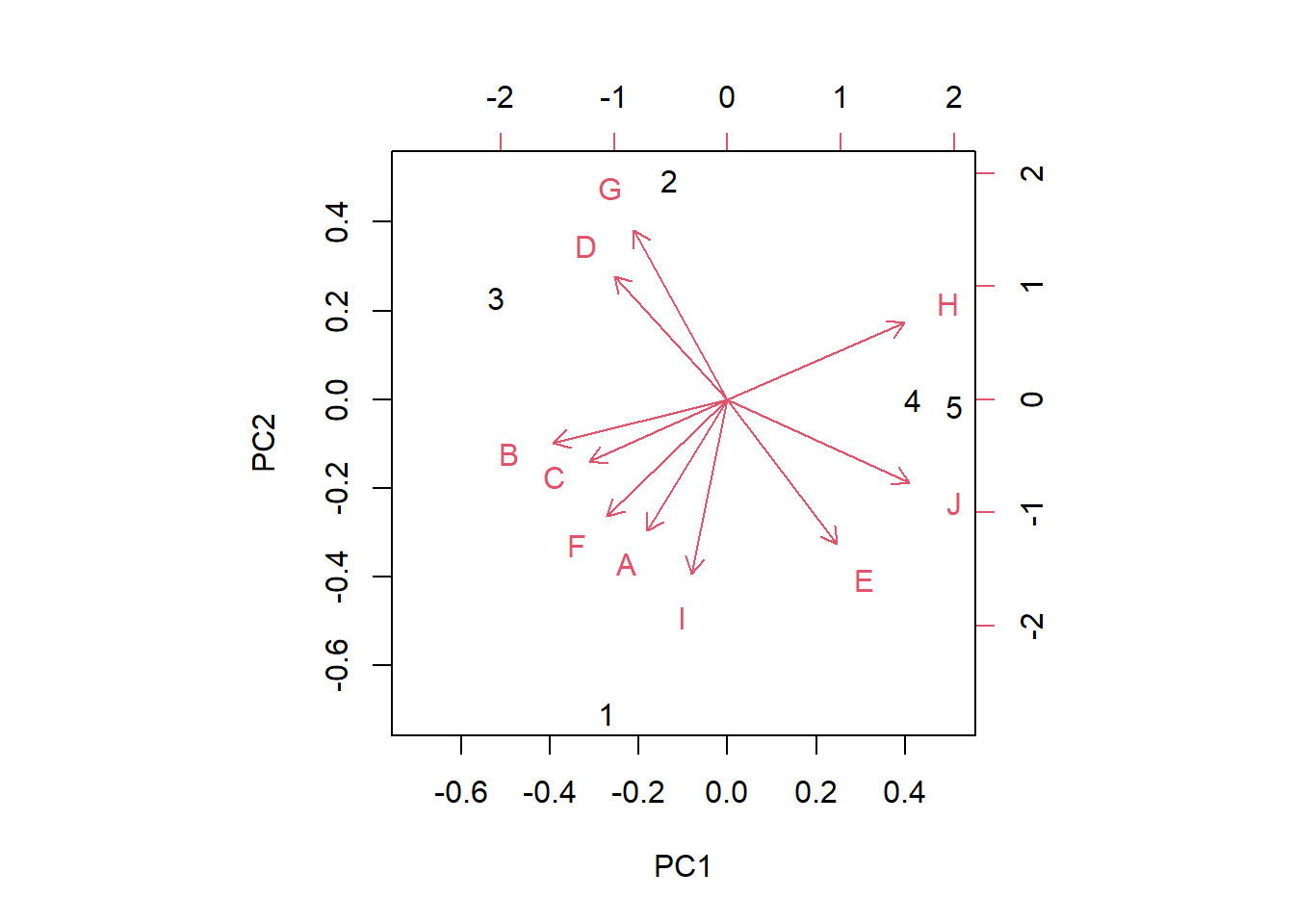

โดยทิศทางที่ชี้ไปนั้นคืออิทธิพลของ Features ดั้งเดิมที่ประกอบเป็น PC

15.3.2 Screeplot

เป็นการพล็อตเพื่อสำรวจว่าแต่ละ PC นั้นมีอิทธิผลจากข้อมูลมากเท่าใด ซึ่งก็คือการดูขนาดของ Eigenvalues หรือ ความแปรปรวนของ PC นั้นๆ

ggplot(data = NULL, aes(x = 1:5)) + 
  geom_col(aes(y = pc$sdev^2),fill = "skyblue", col = "black") +
  geom_line(aes(y = cumsum(pc$sdev^2))) +
  geom_text(aes(y = pc$sdev^2, 
                label = paste0(round(pc$sdev^2,2),"%"), vjust = -2)) +
  labs(x = "PC", y = "Variance (%)") +
  theme_bw()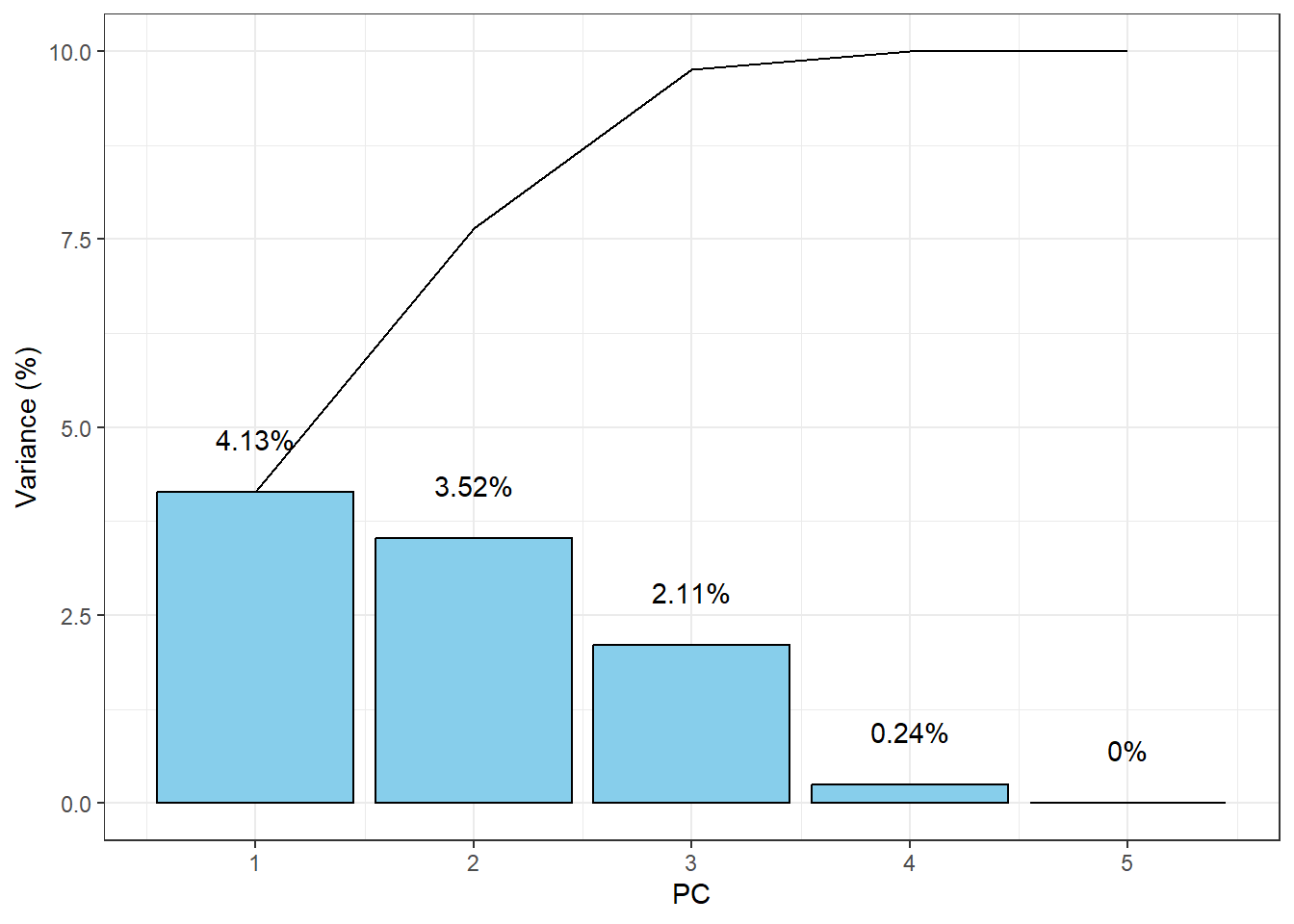

หรือท่านอาจจะเรียก screeplot()

screeplot(pc)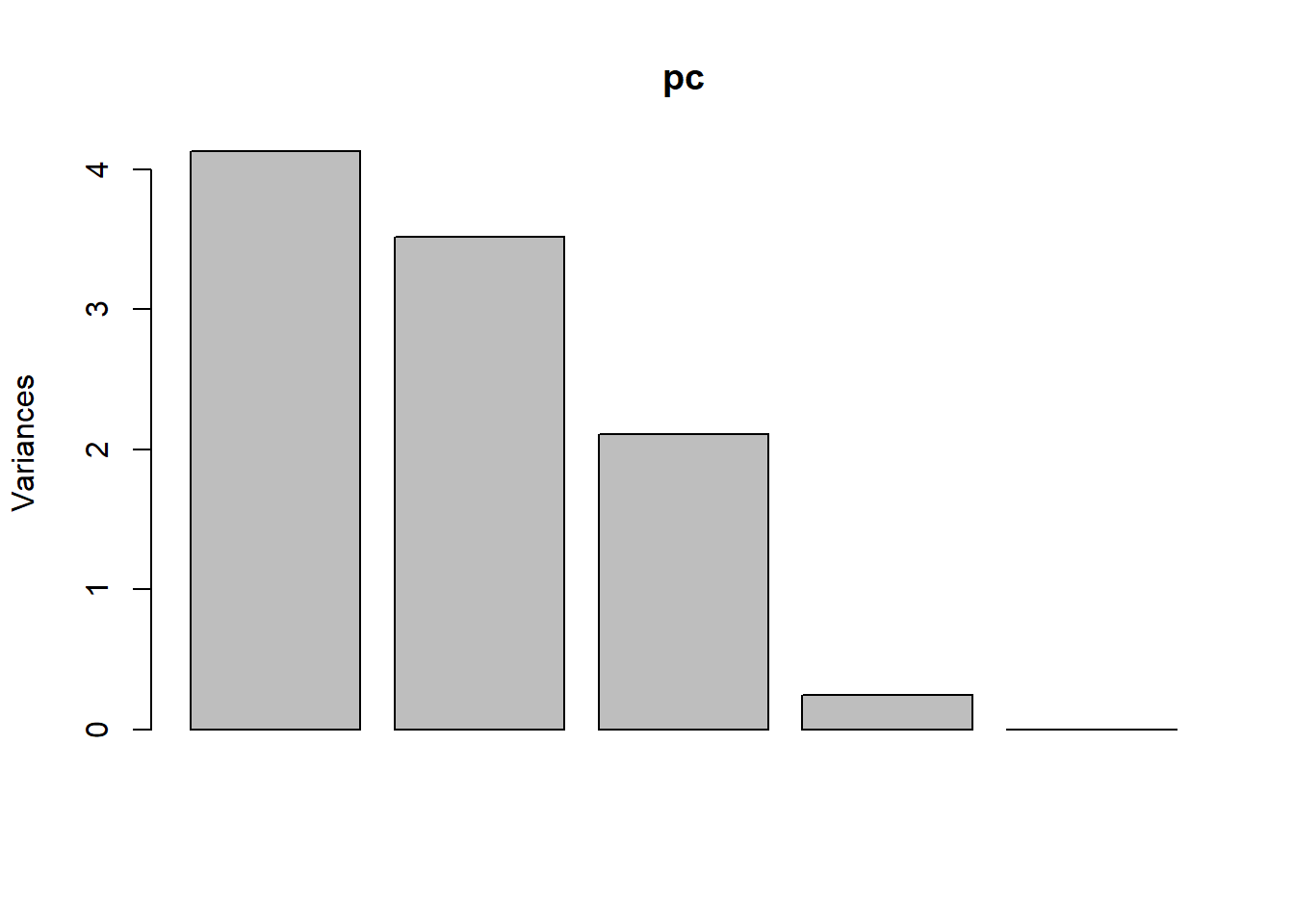

สังเกตว่า PC จะเรียงจากมากไปน้อยเสมอ ตามขนาดของ Eigenvalue

14 Survival analysis

16 Bioconductor