18 edgeR

ผู้นิพนธ์ร่วม: นพ. พงศกร ชูชื่น

18.1 Principle

edgeR (Empirical Analysis with Gene Expression in R) (Chen et al., 2023) เป็น bioconductor package ที่นิยมใช้ในการศึกษา DGE ในการทดลอง RNA-seq ซึ่งตั้งอยู่บนสมมติฐานที่แตกต่างจาก limma เนื่องจากข้อมูล RNA-seq นั้นมีคุณสมบัติที่แตกต่างจากข้อมูลประเภท Microarray ดังนี้

• log(intensity) ของ Microarray ซึ่งเป็นข้อมูล Continuous จึงสามารถใช้โมเดลแบบ Linear ได้ แต่ ข้อมูล RNA-seq นั้นเป็นข้อมูล read count ที่ได้จากการนับ Sequencing จึงเหมาะกับการใช้โมเดลแบบ Poisson มากกว่า

• Heteroscedasticity สูง จึงไม่สามารถใช้สมการถดถอยแบบ Poisson โดยปกติได้

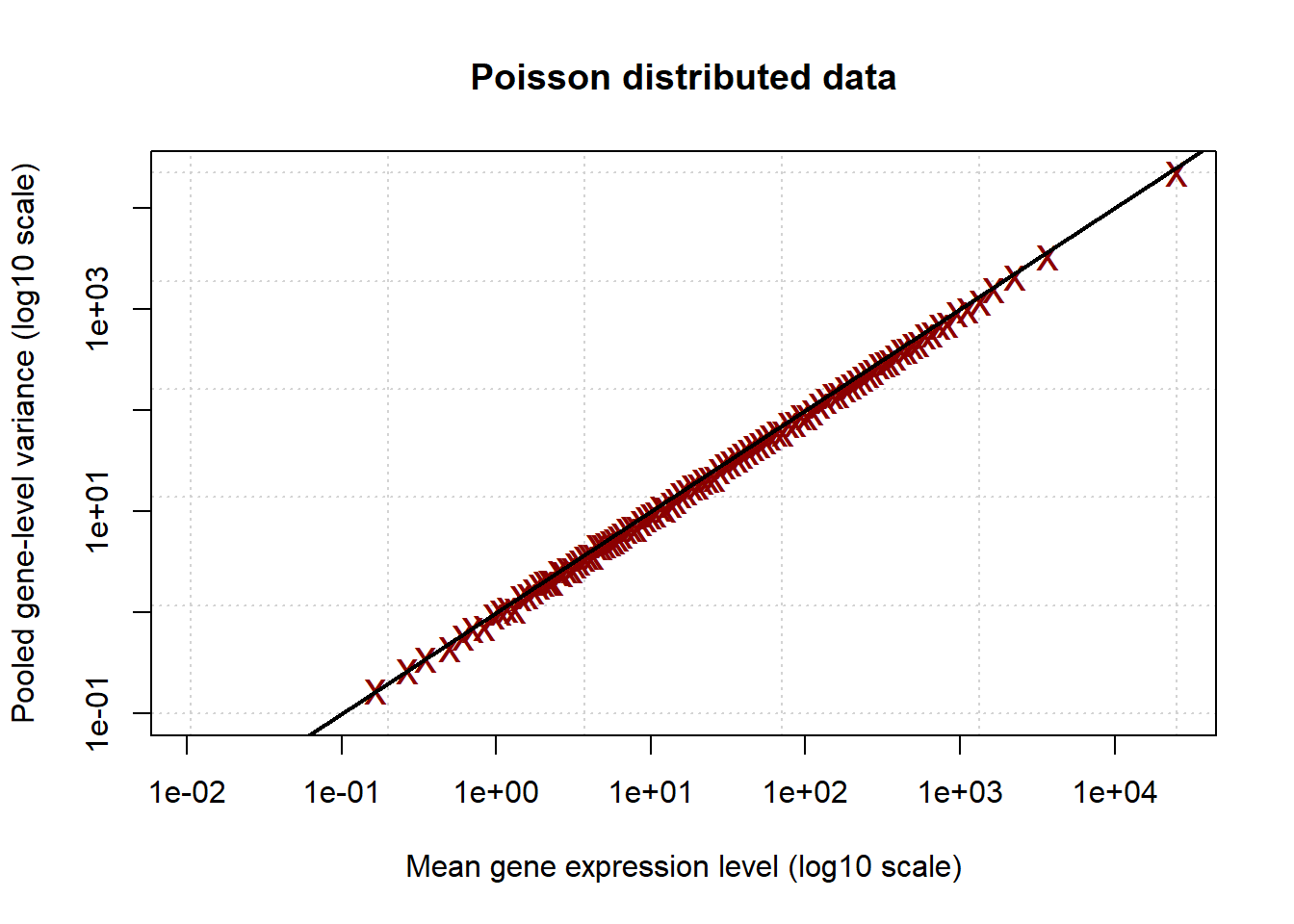
กราฟซ้าย คือความสัมพันธ์ของค่าเฉลี่ยและความแปรปรวนของการกระจายตัวแบบ Poisson โดยทั่วไป ส่วนกราฟขวา เป็นการกระจายตัวของข้อมูล RNA-seq จะเห็นว่าเมื่อค่าเฉลี่ยเพิ่มมากขึ้นนั้น ความแปรปรวนจะเพิ่มในอัตราส่วนที่มากกว่า ทั้งนี้ เนื่องจาก มีปัจจัยของความแปรปรวนที่ไม่ใช่ความแปรปรวนของ Technical variability จากกระบวนการ RNA sequencing (ซึ่งเป็น การกระจายตัวแบบ Poisson) เพียงอย่างเดียว แต่มีความแปรปรวนของ Biological properties ในตัวอย่างมาเกี่ยวข้องด้วย

18.1.1 Negative binomial model

18.1.1.1 Handling biological variation

จากข้อมูลขั้นต้น สมมติฐานของ edgeR คือ RNA-seq มี Technical variation ซึ่งมีการกระจายตัวแบบ Poisson โดยในสถาณการณ์ไม่มี Biological variation ณ ตัวอย่าง \(i\) และ ยีน \(g\) จะมี จำนวนยีน \(y_{gi}\) เท่ากับผลคูณจำนวนยีนทั้งหมดในตัวอย่างนั้น (Total library size; \(N_{i}\)) กับ อัตราส่วนของยีนนั้นๆ ต่อยีนทั้งหมดในตัวอย่าง (\(\pi_{gi}\)) ทั้งหมด \(G\) ยีน ซึ่ง \(\sum_{g=1}^{G}{\pi_{gi}} = 1\) จะได้ว่า

\[ E(y_{gi}) = \mu_{gi} = N_{i}\pi_{gi} \]

อย่างไรก็ตามในข้อมูล RNA-seq นั้นมีส่วนของ Biological variation ในแต่ละตัวอย่างอยู่ ซึ่งทำให้เกิดความแปรปรวนที่นอกเหนือจาก Poisson (Extra-poisson variability) ส่งผลให้เกิดข้อมูลแบบ Overdispersion ซึ่งสมการความสัมพันธ์ระหว่างความแปรปรวนกับค่าเฉลี่ยของ Mixed-poisson distribution คือ

\[ var(y_{gi}) = E_{\pi}[var(y|\pi)] + var_{\pi}[E(y|\pi)] = \mu_{gi} + \phi_{g}\mu^{2}_{gi} \]

\[ CV^{2} = 1/\mu_{gi} + \phi \]

โดยที่ \(\sqrt{1/\mu_{gi}}\) คือ Coefficient variation (\(S/\mu\); CV) จากการกระจายตัวแบบ Poisson ส่วน \(\sqrt{\phi}\) คือ รากที่สองของ CV จากการกระบวนการอื่น ซึ่งในที่นี้คือ Biological properties ของตัว Sample ดังนั้นจะได้ว่า

\[ \text{Total CV}^{2} = \text{Technical CV}^{2} + \text{Biological CV}^{2} \]

สมมติฐานของ edgeR นั้นตั้งอยู่บนพื้นฐานที่ว่า Technical CV นั้นจะลดลงเมื่อจำนวน Sequencing depth นั้นเพิ่มมากขึ้น (\(1/\mu_{gi}\)) แต่ Biological CV นั้นจะยังคงอยู่ไม่ว่า Sequencing depth จะเพิ่มมากขึ้นเท่าไร ดังนั้นสิ่งสำคัญที่เป็นตัวแปรก่อกวนการวัด DGE (ซึ่ง Systemic variability) คือ Biological CV (\(\sqrt{\phi}\)) นั่นเอง

18.1.1.2 Estimation of \(\phi\) and DGE

edgeR ทำการสร้างสมการถดถอย Negative binomial จากการประเมินค่า \(\phi\) โดยวิธีที่เรียกว่า Quantile-adjusted maximum likelihood (qCML) ซึ่งใช้จำนวน Read ทั้งหมดในแต่ละยีนมาสร้างเป็นตาราง Pseudo-count

\[ y_{gi} \sim NB(\mu_{gi}, \phi_{i}) \]

หลังจากนั้น edgeR จะคำนวณ DGE โดยการใช้ Exact test ซึ่งเป็นการรวมโอกาสทั้งหมดที่จะสุ่มได้ Condition ที่ต้องการ ซึ่งวิธีคล้าย Fisher’s exact test ที่มีการคำนึงถึง Effective library size และใช้ Negative binomial distribution แทน Hypergeometric distribution ซึ่งเป็นวิธี Classical method ของ edgeR อย่างไรก็ตาม วิธีนี้มีข้อจำกัดคือสามารถเปรียบเทียบ DGE ได้ระหว่างสองสภาวะเท่านั้น และไม่สามารถจำลองความแปรปรวนอื่นๆ นอกเหนือจากความแปรปรวนของยีนได้

18.1.2 Negative binomial extension

นอกจาก global BCV dispersion แล้ว edgeR ยังสามารถคำนวณ BCV ของแต่ละยีนได้โดยใช้ Quasi-likelihood ของสมการถดถอย Negative binomial

\[ var(y_{gi}) = \sigma^{2}_{g}(\mu_{gi} + \phi\mu_{gi}^{2}) \]

ซึ่งหมายความว่า ทุกๆ ความแปรปรวนของ \(var(y_{gi})\) ที่เพิ่มขึ้นจะถูกทำนายด้วยค่า \(\phi\) (Negative binomial parameter; Global BCV) และ \(\sigma^{2}\) (Quasi-likelihood parameter; Gene-specific BCV) ซึ่งปัญหาของสมการนี้คือจำนวณ Replicate ที่ไม่มากพอในแต่ละยีน edgeR แก้จึงปัญหานี้โดยประยุกต์เทคนิกของ limma มาใช้ ซึ่งก็คือ Empirical Bayes ซึ่งยืมความแปรปรวนมาจากทุกยีนนั่นเอง

18.1.3 Log-linear model

สำหรับข้อมูลที่มีตัวแปรมากกว่าแค่การแสดงออกของยีน หรือมีมากกว่า 2 กลุ่มขึ้นไป จะไม่สามารถประเมิน \(\phi\) โดยใช้วิธี qCML ได้ edgeR จึงทำการประเมิน \(\mu_{gi}\) ด้วยสมการถดถอยเชิงเส้น ซึ่งทำให้สามารถประเมิน \(\mu_{gi}\) ร่วมกับตัวแปรอื่นๆ ได้

\[ log(\mu_{gi}) = \theta_{g_{0}} + \theta_{g_{1}}x_{i_{1}} + \ ... \ + \theta_{g_{n}}x_{i_{n}} + log(N_{i}) \rightarrow \text{offset} \]

\[ y_{gi} \sim NB(\mu_{gi}, \phi_{i}) \]

โดยในสมการนี้จะประเมิน \(\phi\) ด้วยวิธี Cox-Reid profile-adjusted likelihood (cPAL) ซึ่งสามารถจัดการกับข้อมูลแบบ Multivariate ได้ ซึ่งหลังจากนั้นจะสามารถทดสอบ DGE ได้โดย \(F\)-test หรือ Likelihood-ratio test

---

18.2 Workflow

18.3 Example

ในตัวอย่างนี้จะใช้ Bladder gene expression ระหว่าง Tumor และ Control และใช้สมการ Generalized log-linear model

as.data.frame(bladder_mat)

ก่อนอื่นเราต้องสร้าง Condition matrix ซึ่งประกอบด้วย แต่ละ Sample ที่ต้องการศึกษา และ Condition ของตัวอย่างนั้น ซึ่งในที่นี้เราจะแบ่งเป็นสองกลุ่ม ก็คือ Normal และ Tumor

design <- data.frame(
  ID =  colnames(bladder_mat),
  condition = gsub(".{1}$", "", colnames(bladder_mat)) # Remove number
)

design

หลังจากนั้นจะต้องกรองเอายีนที่แสดงออกน้อยออกไป เนื่องจาก Technical variation ของ RNA-seq นั้นมีการกระจายตัวแบบ Poisson นั่นหมายความว่า ยีนที่มีการแสดงออกต่ำนั้นย่อมมี CV ที่สูง อีกทั้ง ยีนที่มีการแสดงออกต่ำนั้นมีโอกาสที่จะถูก Translate ไปเป็นโปรตีนน้อย จึงถือว่าเป็นข้อมูลที่ไม่ค่อยเป็นประโยชน์และเพิ่ม \(\alpha\) error โดยใช่เหตุ จึงสมควรที่จะตัดออกไป โดยค่า Default ของ edgeR นั้นอยู่ที่ 10 counts/sample (จาก Count-per million)

bladder_dge <- DGEList(bladder_mat, group = design$condition) 
keep <- filterByExpr(bladder_dge, min.count = 10)
bladder_dge <- bladder_dge[keep,]

ต่อมา เราจะต้องทำการ Normalize ค่าการแสดงออกของ RNA เนื่องจากการ run RNA seq ในแต่ละ Sample นั้น สภาวะของเครื่องอาจจะมีความแตกต่างกัน ส่งผลให้ค่า Total read count ในแต่ละ Sample มีไม่เท่ากัน โดย edgeR จะใช้วิธี Normalize ที่เรียกว่า Trimmed mean of M-values (TMM) ซึ่งใช้ค่าเฉลี่ยถ่วงน้ำหนักของการแสดงออกยีนในตัวอย่างนั้นๆ หลังจากตัด Outlier ทั้งสูงและต่ำออก (30% ของค่า Log และ 5% ของค่า Absolute)

bladder_dge <- calcNormFactors(bladder_dge)
bladder_dge$samples

หลังจากนั้นจะทำการคำนวณ \(\phi\) ถ้ามี edgeR จะใช้วิธี qCML ถ้าไม่มี Design matrix และใช้วิธี cPAL ถ้ามี Design matrix

model <- model.matrix(~0+condition, data = design)
model

##   conditionN conditionT
## 1          1          0
## 2          1          0
## 3          1          0
## 4          0          1
## 5          0          1
## 6          0          1
## attr(,"assign")
## [1] 1 1
## attr(,"contrasts")
## attr(,"contrasts")$condition
## [1] "contr.treatment"

bladder_dge <- estimateDisp(bladder_dge, design = model)
plotBCV(bladder_dge)

ต่อไปจะทำการ ทดสอบ DGE ด้วยสมการถดถอย ql-nbglm

fit <- glmQLFit(bladder_dge, model)
plotQLDisp(fit)

ตอนนี้จะเห็นว่า BCV ของข้อมูลนั้นถูกบีบมาให้อยู่ใน Trend line จาก Empirical Bayes (Note: edgeR เรียก Function นี้จาก limma)

สุดท้าย เราจะใช้ glmQLFTest() เพื่อวิเคราะห์ \(p\)-value จาก \(F\)-test (สามารถใช้ Likelihood-ratio test ได้ด้วย glmLRT()) และเรียก topTags() เพื่อทำการดึงตารางผลของ DGE ออกมา

genediff <- glmQLFTest(fit, contrast=c(-1,1))
topTags(genediff, n = 100) |> as.data.frame() # First 100 genes

ซึงการแปลผลท้ายสุดจะคล้ายการแปลผลของ limma