9 Hypothesis testing
9.1 Principle
การทดสอบสมมติฐาน คือ การใช้วิธีทางสถิติในตอบคำถามสมมติฐานที่ต้องการ โดยมีขั้นตอน คือ
9.1.1 สร้างสมมติฐาน (Construct the hypothesis)
- สมมติฐานว่าง (Null hypothesis; \(H_{0}\)) คือสมมติฐานที่ต้องการทดสอบ ซึ่งเปรียบเทียบได้กับสิ่งที่ทุกคนมีความเชื่อเดิมอยู่แล้ว (Default belief) หรือไม่ทราบแน่ชัดว่าเป็นอย่างไร ซึ่งจะเป็นแนวปฏิเสธไว้ก่อน คือ ไม่มีความแตกต่างกัน
- สมมติฐานทางเลือก (Alternative hypothesis; \(H_{a}\)) คือสมมติฐานที่คาดหวังว่าจะเป็นการค้นพบใหม่
9.1.2 ทำการวิเคราะห์ค่าทางสถิติ (Construct the test statistics)
โดยเครื่องมือจะมีหลายรูปแบบตามลักษณะของข้อมูล เช่น t-test, Chi-square เป็นต้น ซึ่งผลลัพธ์จากการหาค่าทางสถิติจะเป็นไปตามการทดสอบนั้นๆ เช่น \(t\)-test: \(t\), Chi-square: \(X^{2}\), \(F\)-test: \(F\) เป็นต้น
9.1.3 หา \(p\)-value
คือ โอกาสที่สามารถสังเกตค่าทางสถิติที่มากกว่าค่าการวิเคราะห์ทางสถิติที่โดยไม่ได้อยู่ภายใต้ \(H_{0}\) โดยทางปฏิบัติแล้วคือ การสร้างแบบจำลองข้อมูลภายใต้ \(H_{0}\) ขึ้นมาแล้วแล้วดูว่า ที่ค่าสถิตินั้น มีโอกาสไม่เกิดเท่าไร
ยกตัวอย่าง เมื่อวิเคราะห์ \(t\)-test จะทำการสร้าง t-distribution ขึ้นมา (ตัวอย่างของการวิเคราะห์ อยู่บทถัดไป ) ภายใต้ \(H_{0}\) ว่า mean = 10
library(tidyverse)
t_dist <- dt(seq(-5,5,0.01), df = 99) # t-distribution มี mean = 0 sd = 1
tval <- 0.7345 # t-value วิธีคำนวณอยู่ในบท t-test
density_df <- data.frame(x = seq(-5,5,0.01), y = t_dist) |>
mutate(area = ifelse(between(x,-tval,tval), TRUE,FALSE))
ggplot(density_df, aes(x,y)) +
geom_area(fill = "skyblue", color = "black") +
geom_area(data = filter(density_df, area), fill = "white", color = "black") +
geom_vline(xintercept = c(-tval,tval), linetype = "dashed") +
theme_bw()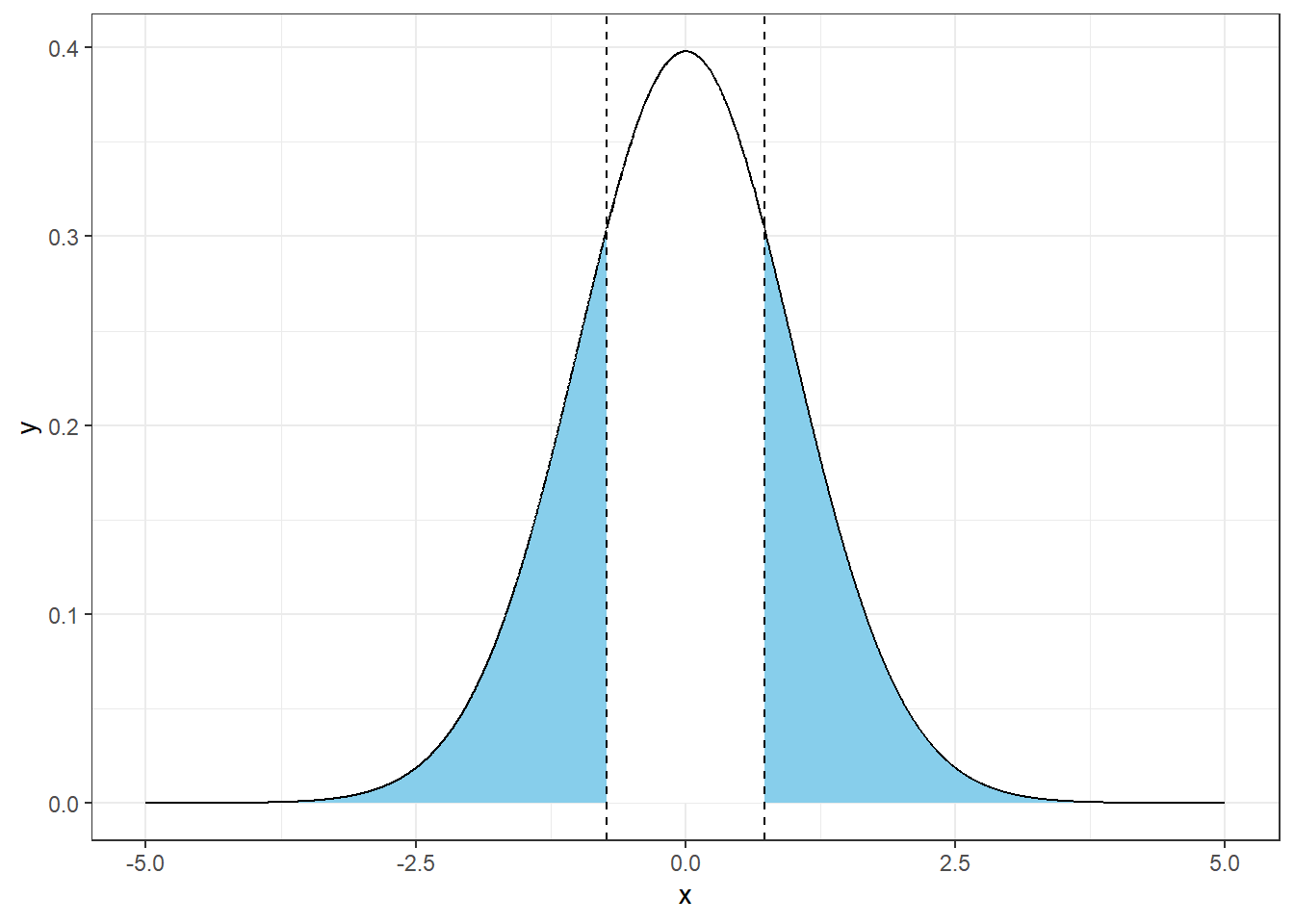
- ที่ -0.7345 < \(t\) < 0.7345 (พื้นที่ใต้กราฟสีขาว) หมายถึงโอกาสที่ค่านั้นเกิดจากความบังเอิญภายใต้ \(H_{0}\) ที่ยังเป็นจริง คิดเป็น AUC ได้
## [1] 53.59248- ที่ \(t\) < -0.7345 หรือ \(t\) > 0.7345 (พื้นที่ใต้กราฟสีฟ้า) หมายถึงโอกาสที่ค่านั้นไม่ได้เกิดจากความบังเอิญภายใต้ \(H_{0}\) ที่ยังเป็นจริง (Extreme value) คิดเป็น AUC ได้
## [1] 46.40728
p <- 2*pt(0.7345, 99, lower.tail = FALSE)
p # p-value## [1] 0.4643803โดย AUC_blue = \(p\)-value = พื้นที่ใต้กราฟสีฟ้า = ~46.4%
9.1.4 เปรียบเทียบ \(p\)-value กับ ค่าวิกฤติ (Critical value) ที่ยอมรับได้
จุดนี้จะเป็นการตัดว่า ท่านสามารถยอมรับความบังเอิญนี้ที่กี่ % โดยทั่วไปมักใช้ที่น้อยกว่า 5% (0.05) หรือ 1% (0.01) ซึ่งแบ่งเป็น
Left-tailed คือ โอกาสที่ Critical value \(\leq H_{0}\)
Right-tailed คือ โอกาสที่ Critical value \(\geq H_{0}\)
Two-tailed คือ โอกาสที่ Critical value \(\neq H_{0}\) นิยมใช้วิเคราะห์มากที่สุด
crit <- qt(1-0.05/2, df = 99) # ตัดที่ <= p 0.05, two-tailed
density_df <- density_df |>
mutate(crits = ifelse(between(x,-crit,crit), TRUE,FALSE))
ggplot(density_df, aes(x,y)) +
geom_area(fill = "darkred", color = "black") +
geom_area(data = filter(density_df, crits),
fill = "skyblue", color = "black") +
geom_area(data = filter(density_df, area),
fill = "white", color = "black") +
geom_vline(xintercept = c(-tval,tval), linetype = "dashed") +
geom_vline(xintercept = c(-crit,crit), linetype = "dashed", color = "red") +
theme_bw()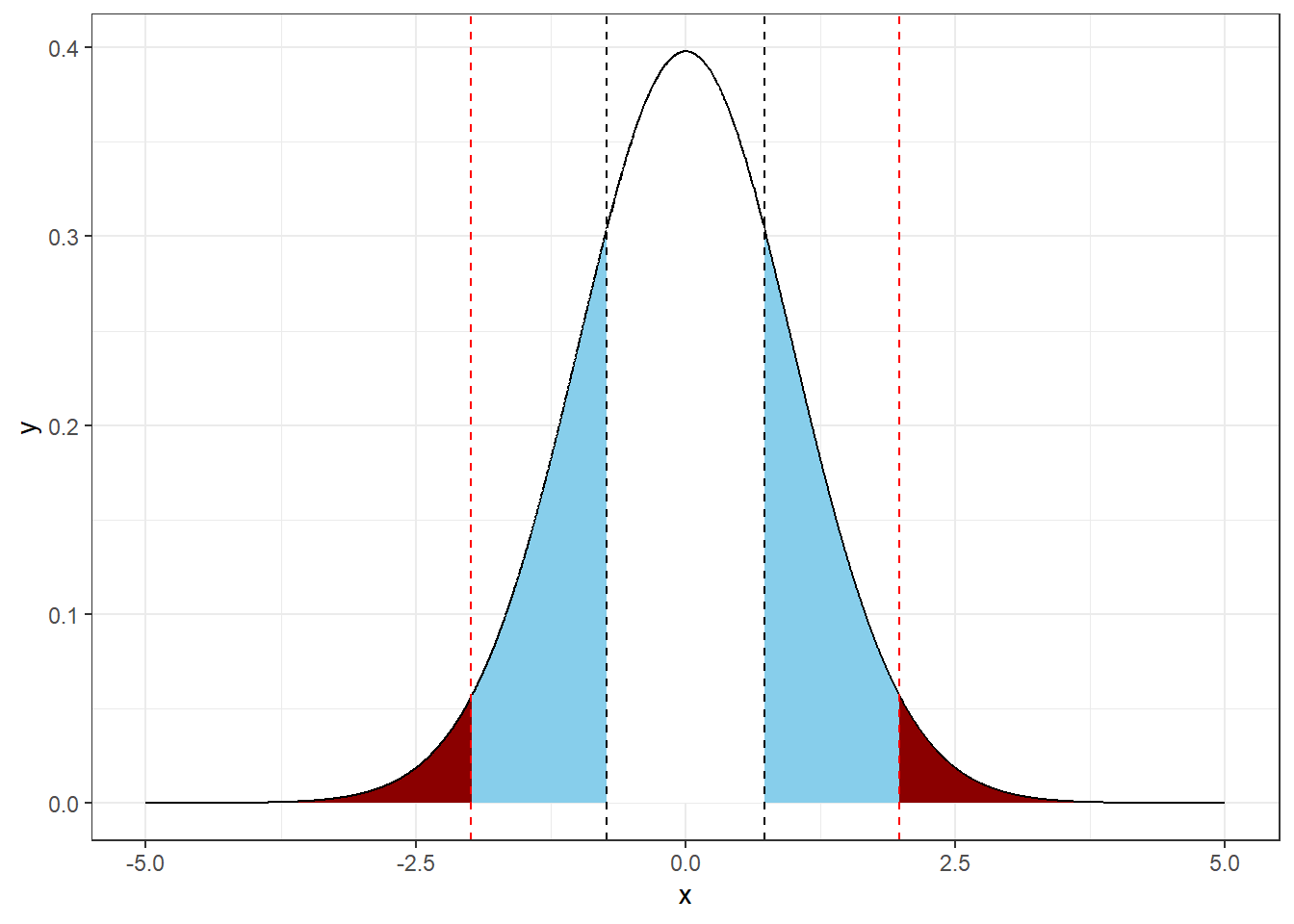
จะเห็นว่า โอกาสที่ความแตกต่างนั้นไม่ได้เกิดจากความบังเอิญภายใต้ \(H_{0}\) นั้นอยู่ที่ 46% ซึ่งมากกว่า 5% ที่ต้องการ จึงไม่สามารถปฏิเสธ \(H_{0}\) ได้ เรียกอีกแบบหนึ่งว่า ไม่ได้แตกต่างอย่างมีนัยสำคัญ (จนสามารถปฏิเสธ \(H_{0}\) ได้)
ตรงส่วนพื้นที่ระหว่าง Critical value (ระหว่างเส้นประสีแดง) คือ พิสัยของความแตกต่างที่สามารถรับได้ ซึ่งจะถูกนำไปใช้ในการคำนวณค่าความเชื่อมั่น (Confidence interval)
\[ CI = \text{Estimate } \pm \text{Test statistics}\times SE \]
Power
คือ โอกาสการเกิดผลบวกจริง (True positive) ของ \(H_{a}\) = 1 - Power
พิจารณาการคำนวณทางสถิติ t-test ภายใต้สมมติฐาน \(H_{0}\): \(\mu = 12\) และ \(H_{a}\): \(\mu > 12\) ที่ \(S = 1.7\)
## [1] 1.378737
t_test_5 <- t.test(mean_5_sample, mu = 12, alternative = "greater")
t_test_5##
## One Sample t-test
##
## data: mean_5_sample
## t = 2.1555, df = 4, p-value = 0.04869
## alternative hypothesis: true mean is greater than 12
## 95 percent confidence interval:
## 12.01459 Inf
## sample estimates:
## mean of x
## 13.32907จากการคำนวณ สามารถสรุปได้ว่าสามารถปฏิเสธ \(H_{0}\) นั่นคือ ข้อมูลของกลุ่มตัวอย่างนี้มีค่าเฉลี่ยมากกว่าจาก 12 อย่างมีนัยสำคัญ แต่ว่า \(H_{a}\) นั้น มีโอกาสเป็นจริงหรือไม่นั้น เมื่อพิจารณาของกระจายตัวของข้อมูล t-distribution แล้ว
library(pwrss)
power.t.test(ncp = t_test_5$statistic, df = 4, alpha = 0.05,
alternative = "greater", plot = TRUE, verbose = FALSE)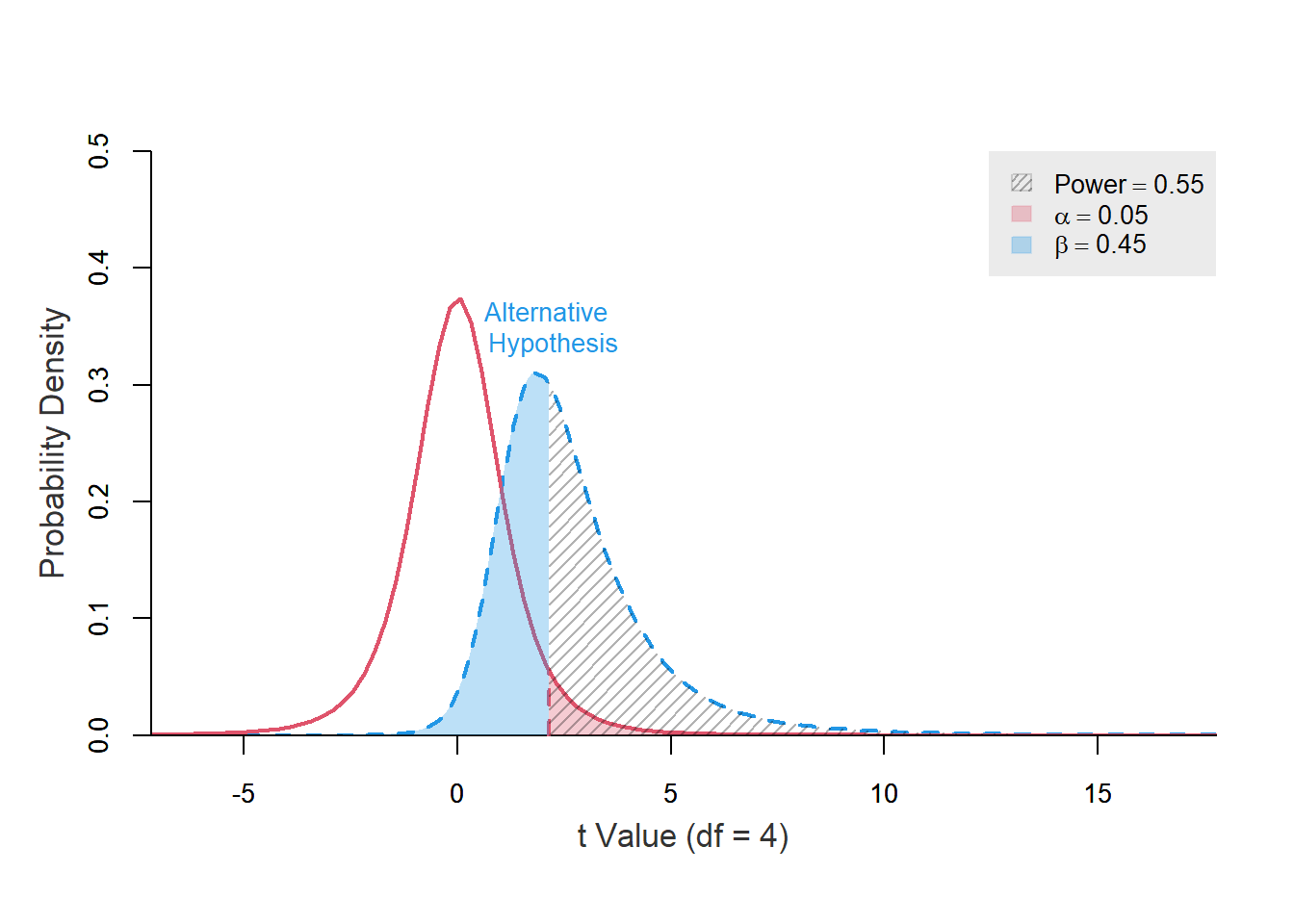
จากกราฟ เส้นประสีแดงคือการกระจายตัวของข้อมูล \(H_{0}\): \(\mu = 12\) ส่วนเส้นประสีฟ้าคือ \(H_{a}\): \(\mu = 12 + \frac{1.379}{4}\times2.156 = 12.743\) พื้นที่สีแดงคือ Critical value = \(\alpha\) ที่ 0.05
ดังนั้น พื้นที่สีฟ้าคือ พื้นที่ของกลุ่มตัวอย่างจาก \(H_{a}\): \(\mu = 12.743\) ซึ่งแท้จริงแล้ว สามารถอยู่ในกลุ่ม \(H_{0}\): \(\mu = 12\) ได้เช่นกัน ซึ่งก็คือโอกาสการเกิดผลบวกลวง (False positive) = Type-II error นั้นเอง
ส่วนตรงที่เป็นเส้นแนวเฉียงสีฟ้า คือพื้นที่ๆ ไม่มีทางมาจาก \(H_{0}\) ได้ ซึ่งก็คือ ความสามารถในการแยกแยะกลุ่มตัวอย่างที่เป็นความจริง เรียกว่า ผลบวกที่แท้จริง (True positive) = Power = 1 - Type-II error ดังนั้น ถ้าท่านเพิ่มค่า \(\alpha\) สูงสุดที่รับได้ โอกาสการเกิด False positive ก็จะเพิ่มขึ้น แต่โอกาสการเกิด False negative ก็จะต่ำลง (= Power สูงขึ้น)
power.t.test(ncp = t_test_5$statistic, df = 4, alpha = 0.1,
alternative = "greater", plot = TRUE, verbose = FALSE)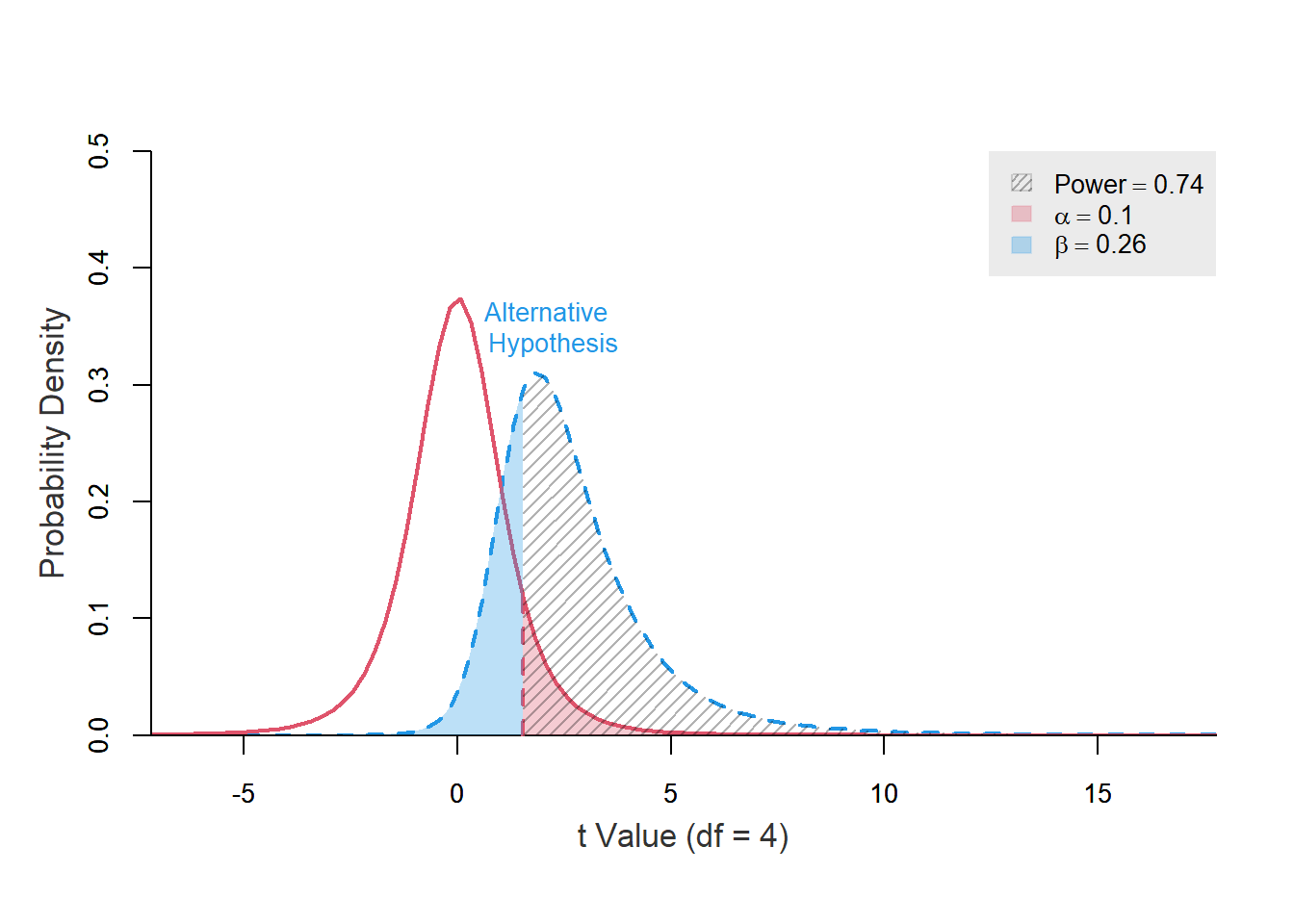
อย่างไรก็ตาม ในด้านงานวิจัยนั้น ส่วนใหญ่จะให้ความสำคัญกับ False positive มากกว่า เนื่องจากผลบวกลวงอาจจะส่งผลให้ตัดสินใจเปลี่ยนแปลงการรักษาเดิมที่เป็นมาตรฐาน ซึ่งอาจเกิดผลเสียแก่ผู้ป่วยได้ ดังนั้น จึงไม่ค่อยมีการปรับเพิ่ม \(\alpha\) แต่จะเลือกเพิ่ม Power จากการเพิ่ม Sample size มากกว่า โดยจำนวนตัวอย่างที่มากขึ้น ส่งผลให้ความแปรปรวนในการวัด (Standard error) ลดลง ส่งผลให้การกระจายตัวของข้อมูลนั้นแคบลงด้วย
## [1] 1.653531## [1] 0.3697408
t_test_20 <- t.test(mean_20_sample, mu = 12, alternative = "greater")
t_test_20##
## One Sample t-test
##
## data: mean_20_sample
## t = 3.3558, df = 19, p-value = 0.00166
## alternative hypothesis: true mean is greater than 12
## 95 percent confidence interval:
## 12.60143 Inf
## sample estimates:
## mean of x
## 13.24076
power.t.test(ncp = t_test_20$statistic, df = 19, alpha = 0.05,
alternative = "greater", plot = TRUE, verbose = FALSE) 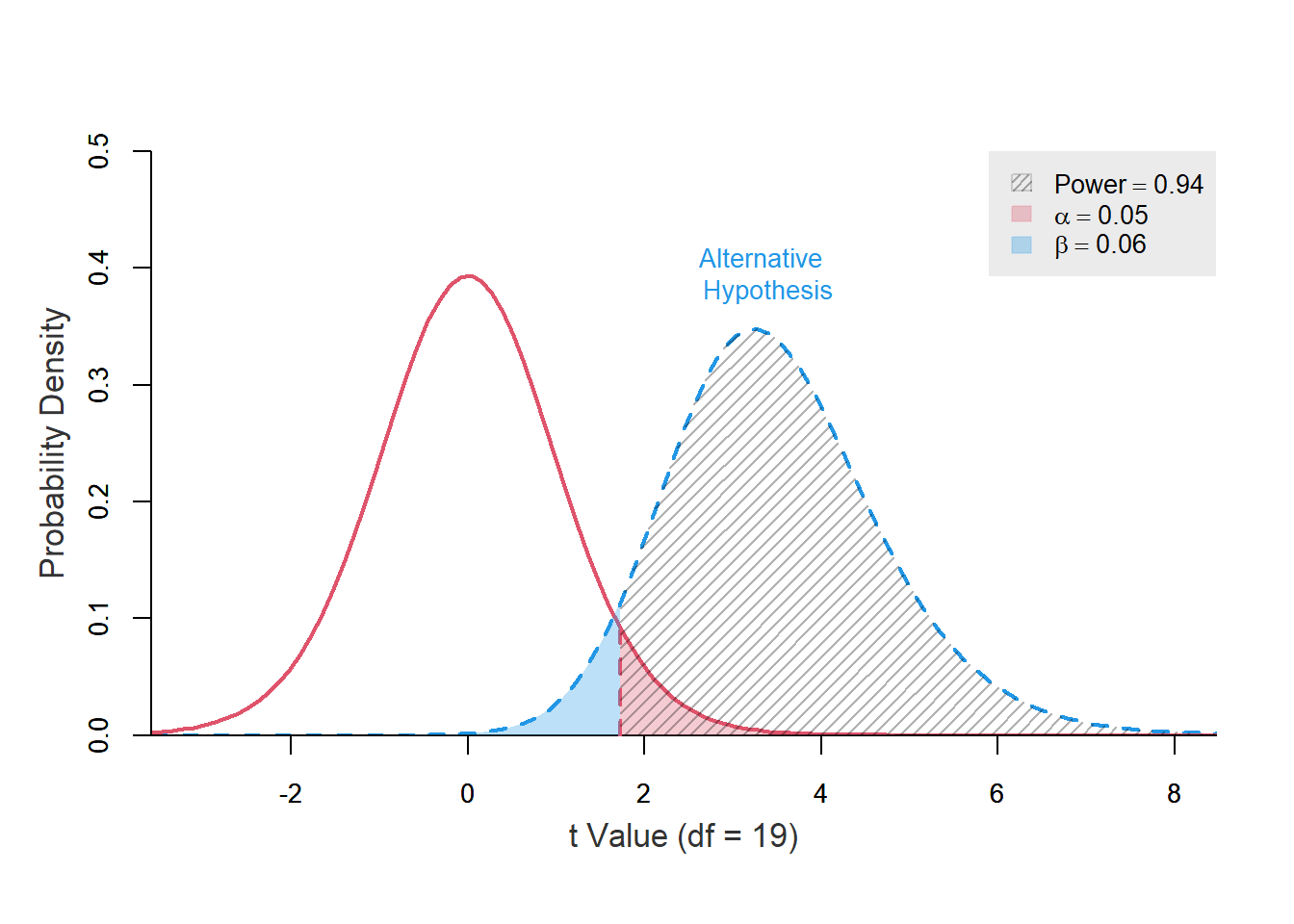
จากกราฟ เส้นประสีแดงคือการกระจายตัวของข้อมูล \(H_{0}\): \(\mu = 12\) ส่วนเส้นประสีฟ้าคือ \(H_{a}\): \(\mu = 12 + \frac{1.654}{19}\times3.356 = 12.29\) พื้นที่สีแดงคือ Critical value = \(\alpha\) ที่ 0.05 จะเห็นว่าการกระจายตัวของข้อมูลทั้งสองกลุ่มนั้นแคบกว่า (สังเกตตัวเลขแกน x) จึงมีส่วนที่พื้นที่ร่วมกันที่น้อยกว่าด้วย
เมื่อพล็อตกราฟความสัมพันธ์ระหว่าง ขนาดตัวอย่าง, \(\alpha\), Power จะได้ดังรูป
mean_diff <- 1 # ความต่างคงที่ 1
n <- 3:50
alphas <- c(0.5, 0.2, 0.1,0.05,0.01,0.001)
power_df <- expand_grid(n = n, alphas = alphas) |>
mutate(power = stats::power.t.test(n = n, delta = mean_diff, sig.level = alphas, sd = 1)$power) |>
mutate(alpha = as.factor(alphas)) |>
mutate(alpha = fct_reorder(alpha, desc(alphas)))
ggplot(power_df, aes(x = n, y = power, col = alpha, linetype = alpha)) +
geom_line(linewidth = 1.25) + theme_bw() +
labs(y = "Power (1-beta)", x = "Sample size")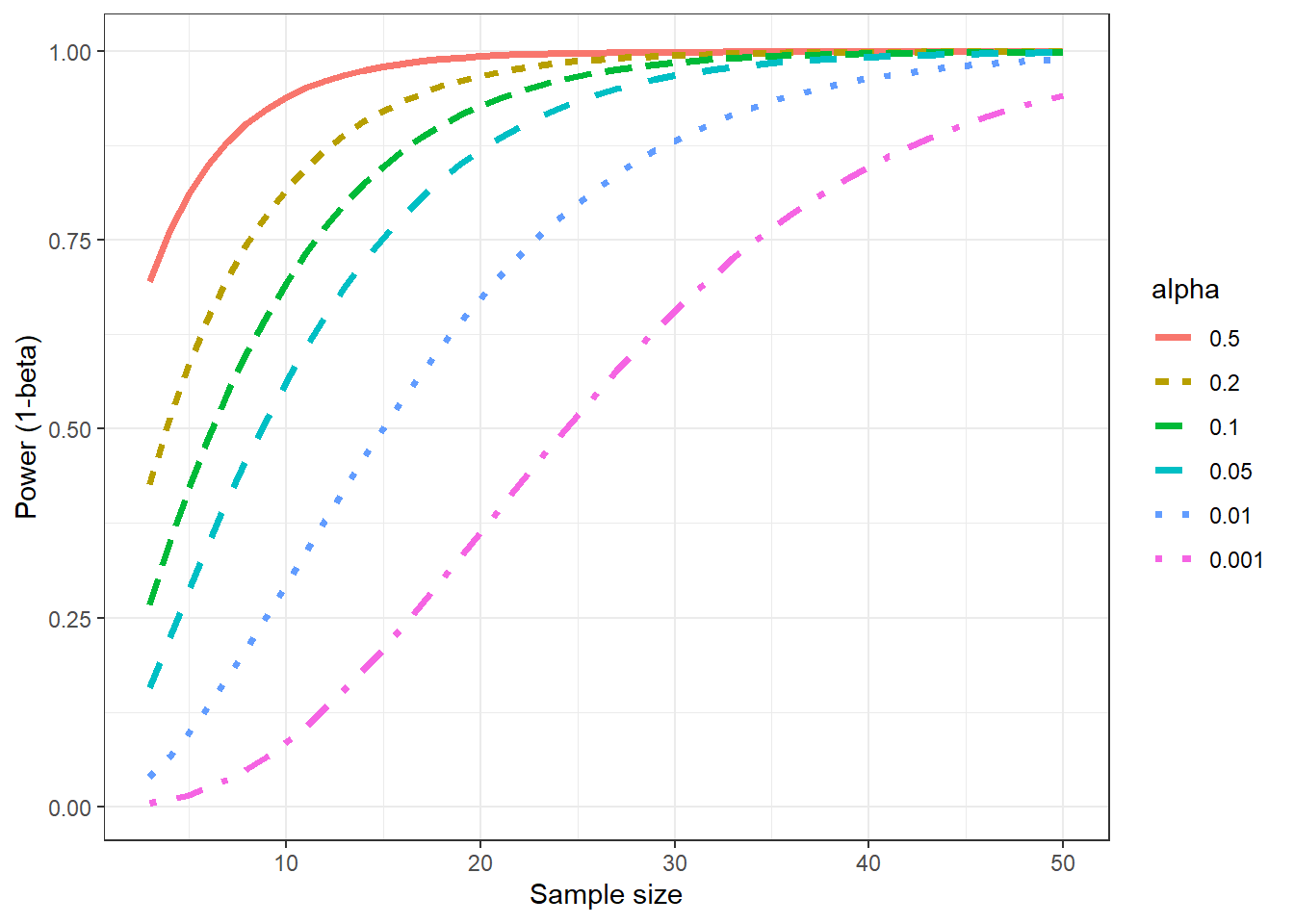
Note: ทั้งหมดนี้เป็นการคำนวณตัวอย่างของ t-test เท่านั้น การกระจายตัวแบบอื่นจะมีวิธีคำนวณ Power ที่ต่างกันไป อย่างไรก็ตามหลักการพื้นฐานจะคล้ายกัน
Trade-off ของ p-value threshold
การตั้งค่าวิกฤตินั้นมี Trade-off ระหว่าง False positive และ False negative ที่ต้องพิจารณา
| Decision/Truth | \(H_{0}\) | \(H_{a}\) |
|---|---|---|
| Reject \(H_{0}\) | Type I error | Correct |
| Accept \(H_{0}\) | Correct | Type II error |
Type I error = False positive = \(\alpha\) = Critical value
Type II error = False negative = \(\beta\) = 1 - Power
\(\therefore\) Power = True positive