10 Parametric test

คือ การวิเคราะห์ทางสถิติที่เราทราบลักษณะการกระจายตัวของข้อมูลอย่างชัดเจน แต่มีข้อดีคือการเปรียบเทียบข้อมูลจะมีความแม่นยำสูง

10.1 \(t\)-test

คือ การคำนวณทางสถิติที่เปรียบเทียบค่าเฉลี่ย (Mean) และความผันผวนของการวัด (Standard Error; SE) ระหว่างสองกลุ่ม แบ่งเป็น

10.1.1 One sample \(t\)-test

เป็นการเปรียบเทียบความแตกต่างของค่าเฉลี่ยระหว่างกลุ่มตัวอย่าง (Sample) กับประชากร (Population)

\[ t = \frac{\bar{x} - \mu_{0}}{SE} = \frac{\bar{x} - \mu_{0}}{s/\sqrt{n}} \]

เพื่อให้เห็นภาพของความต่างในการทดสอบนี้ เราจะทำการสร้างกราฟเปรียบว่ากลุ่มตัวอย่างนั้น มีค่าเฉลี่ยต่างจากประชากร ที่ ค่าเฉลี่ย = 10 และ ค่าเฉลี่ย = 30 หรือไม่

set.seed(123)
norm_10_pop <- rnorm(1000, mean = 10, sd = 4) # สร้างประชากร mean = 10, sd = 4
norm_10_sample <- sample(norm_10_pop, 100) # สุ่มตัวอย่างมาจากประชากร 100 ราย
norm_30_pop <- rnorm(1000, mean = 30, sd = 4)
norm_30_sample <- sample(norm_30_pop, 100)

norm_pop_df <- data.frame(Pop_10 = norm_10_pop, Pop_30 = norm_30_pop) |>
  pivot_longer(everything(), names_to = "Pop", values_to = "Values")  

norm_sample_df <- data.frame(Samp_10 = norm_10_sample, Samp_30 = norm_30_sample) |>    pivot_longer(everything(), names_to = "Samp", values_to = "Values")  

ggplot(norm_pop_df, aes(x = Values, fill = Pop)) +    
  geom_density(aes(y = after_stat(count)),color = "black", alpha = 0.5) + 
  geom_density(data = norm_sample_df, 
               aes(x  = Values, y = after_stat(count), fill = Samp), 
               color = "black", alpha = 0.7) + theme_bw()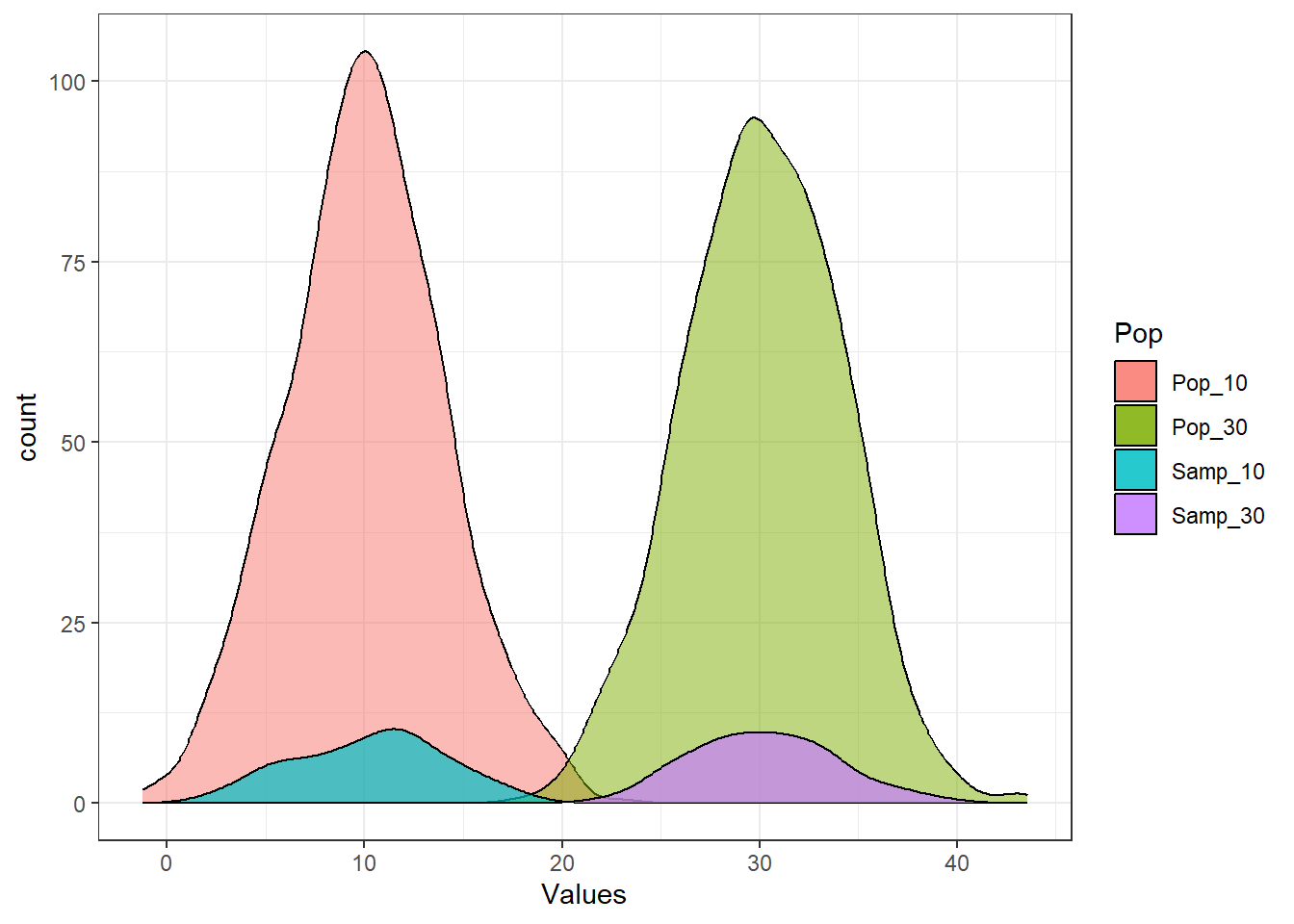

จะเห็นว่าเมื่อดูลักษณะการกระจายตัวของข้อมูลแล้ว Samp_10 ที่มี ค่าเฉลี่ย = 10 นั้น ไม่ต่างจากประชากรที่มี ค่าเฉลี่ย = 10 แต่ดูแตกต่างอย่างเห็นได้ชัดกับประชากรที่มี mean = 30 t.test จะช่วยตัดสินว่าค่าที่ได้นั้นแตกต่างกันจริงหรือไม่ โดยสมมติฐานที่ตั้งคือ

Case 1: ประชากรมีค่าเฉลี่ย = 10

\(H_{0}\): ค่าเฉลี่ยของกลุ่มตัวอย่างนั้น ไม่ต่างจากค่าเฉลี่ยของประชากร = 10
\(H_{a}\): ค่าเฉลี่ยของกลุ่มตัวอย่างนั้น ต่างจากค่าเฉลี่ยของประชากร = 10

t.test(norm_10_sample, mu = 10) # p > 0.05

## 
##  One Sample t-test
## 
## data:  norm_10_sample
## t = 0.73547, df = 99, p-value = 0.4638
## alternative hypothesis: true mean is not equal to 10
## 95 percent confidence interval:
##   9.533936 11.015052
## sample estimates:
## mean of x 
##  10.27449

Case 2: ประชากรมีค่าเฉลี่ย = 40

\(H_{0}\): ค่าเฉลี่ยของกลุ่มตัวอย่างนั้น ไม่ต่างจากค่าเฉลี่ยของประชากร = 40
\(H_{a}\): ค่าเฉลี่ยของกลุ่มตัวอย่างนั้น ต่างจากค่าเฉลี่ยของประชากร = 40

t.test(norm_10_sample, mu = 30) # p <= 0.05

## 
##  One Sample t-test
## 
## data:  norm_10_sample
## t = -52.852, df = 99, p-value < 2.2e-16
## alternative hypothesis: true mean is not equal to 30
## 95 percent confidence interval:
##   9.533936 11.015052
## sample estimates:
## mean of x 
##  10.27449

จะเห็นว่าต่างจากประชากรที่ค่าเฉลี่ย = 30 อย่างมีนัยสำคัญ (\(p\) = \(2.2 \times 10^{-16}\) < Critical point = 0.05)

พิจารณาที่มาของ \(p\)-value นั้นมีที่มาจากสูตรขั้นต้น

hypothesized_mean <- 30
mean_sample <- mean(norm_10_sample)
sd_sample <- sd(norm_10_sample)

t <- (mean_sample - hypothesized_mean)/(sd_sample/sqrt(length(norm_10_sample)))

t

## [1] -52.85159

2*pt(t, df = 99) # p-value

## [1] 2.306252e-74

จะเห็นว่าค่า \(t\) นั้นเท่ากับ ค่าที่ได้จาก t.test ขั้นต้น เมื่อสร้าง \(t\)-distribution ที่มี \(H_{0}\) คือ ค่าเฉลี่ย = 0 แล้วจะพบว่าค่านี้มากกว่า Critical value

10.1.2 Independent t-test

เป็นการเปรียบเทียบค่าเฉลี่ยระหว่าง ตัวอย่างสองกลุ่มที่ไม่เกี่ยวเนื่องกัน

\[ t = \frac{\bar{x_{1}}-\bar{x_{2}}-\mu_{0}}{\sqrt{\frac{s^{2}_1}{n_{1}}+\frac{s^{2}_2}{n_{2}}}} \]

\[ s_{p} = \sqrt{\frac{(n_{1}-1)s^{2}_{1}+(n_{2}-1)s^{2}_{2}}{{n_{1}} + n_{2} - 2}} \]

กลับไปดูภาพขั้นต้น ครั้งนี้จะเทียบระหว่างกลุ่มตัวอย่างสองกลุ่ม คือ norm_10_sample และ norm_30_sample ว่ามี ค่าเฉลี่ยที่แตกต่างกันอย่างมีนัยสำคัญหรือไม่

\(H_{0}\): ค่าเฉลี่ยของ norm_10_sample และ norm_30_sample นั้นไม่แตกต่างกัน (\(\bar{x_{1}} - \bar{x_{2}} = 0\))
\(H_{a}\): ค่าเฉลี่ยของ norm_10_sample และ norm_30_sample นั้นแตกต่างกัน (\(\bar{x_{1}} - \bar{x_{2}} \neq 0\))

t.test(norm_10_sample, norm_30_sample, var.equal = TRUE)

## 
##  Two Sample t-test
## 
## data:  norm_10_sample and norm_30_sample
## t = -38.469, df = 198, p-value < 2.2e-16
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -20.93623 -18.89440
## sample estimates:
## mean of x mean of y 
##  10.27449  30.18981

สรุปได้ว่าค่าเฉลี่ยของกลุ่มตัวอย่างทั้งสองกลุ่มนั้นแตกต่างกันอย่างมีนัยสำคัญ

ลองคำนวณเอง

ind_t_df <- data.frame(ten = norm_10_sample, thirty = norm_30_sample) |> 
  summarize(across(c(everything()), .fns = 
                     list(mean = mean, sd = sd)))
ind_t_df

ind_t_se <- with(ind_t_df, sqrt( (ten_sd^2)/100 + (thirty_sd^2)/100 ) )
ind_t_se

## [1] 0.5176993

ind_t <- (ind_t_df$ten_mean - ind_t_df$thirty_mean - 0)/ind_t_se
ind_t

## [1] -38.46889

pt(ind_t, df = length(norm_10_sample) + length(norm_30_sample)-2)*2

## [1] 7.928494e-94

Note: บางครั้งข้อมูลอาจจะมีความแปรปรวนไม่เท่ากัน ในที่นี้มักจะใช้ Welch’s \(t\)-test โดย t.test(…, var.equal = FALSE) โดยสมการนี้จะทำการปรับความแปรปรวนให้ด้วย

10.1.3 Paired t-test

เป็นการเปรียบเทียบค่าเฉลี่ยระหว่างตัวอย่างสองกลุ่มที่เกี่ยวเนื่องกัน (ก่อน-หลัง แม่-ลูก เป็นต้น)

\[ t = \frac{\bar{x}_{d}-\mu_{0}}{s_{x_{d}}/\sqrt{n}} \]

\[ x_{di} = x_{1_{i}}-x_{2_{i}} \]

\[ s_{x_{d}} = \sqrt{\frac{\sum_{d=1}^{n}(x_{d}-\bar{x}_{d})^{2}}{(n-1)}} \]

t.test(norm_10_sample, norm_30_sample, paired = TRUE, var.equal = TRUE)

## 
##  Paired t-test
## 
## data:  norm_10_sample and norm_30_sample
## t = -37.802, df = 99, p-value < 2.2e-16
## alternative hypothesis: true mean difference is not equal to 0
## 95 percent confidence interval:
##  -20.96067 -18.86996
## sample estimates:
## mean difference 
##       -19.91532

จะเห็นว่ามีความแตกต่างในส่วนของ \(df\) (Degree of freedom) ซึ่งเกิดจากการจับคู่หาความต่าง 100 ครั้ง เนื่องจากค่าที่เปรียบเทียบนั้นอยู่ในตัวอย่างเดียวกัน (แม่ลูก คู่ที่ 1 แม่ลูกคู่ที่ 2 … เป็นต้น) เมื่อเปรียบเทียบกับ Independent \(t\)-test เนื่องจากเป็นการหา mean ในกลุ่มของตัวเอง 2 ครั้ง และมาเทียบความต่างกัน

ลองคำนวณเอง

paired_t_df <- data.frame(ten = norm_10_sample, thirty = norm_30_sample) |> 
  mutate(diff = ten -thirty) |> 
  mutate(mean_diff = mean(diff)) |> 
  mutate(ss_mean_diff = (diff-mean_diff)^2)

paired_t_df

t_sd <- (sum(paired_t_df$ss_mean_diff)/(nrow(paired_t_df)-1) ) |> sqrt()
t_sd

## [1] 5.268367

t_paired <- mean(paired_t_df$diff)/(t_sd/sqrt(nrow(paired_t_df)))
t_paired

## [1] -37.80168

pt(t_paired, df = nrow(paired_t_df)-1)*2

## [1] 1.223407e-60

ดังนั้น การเลือก Paired vs Independent นั้นมีความสำคัญ ขึ้นอยู่กับโจทย์การศึกษาของท่านด้วย

10.2 Analysis of Variance (ANOVA)

คือ การคำนวณทางสถิติที่เปรียบเทียบค่าเฉลี่ยและความแปรปรวนระหว่างสองกลุ่มขึ้นไป โดยมีสมมติฐาน คือ

\(H_{0}\): ค่าเฉลี่ยของทุกกลุ่มเท่ากัน (\(\bar{x_{1}} = \bar{x_{2}} = \bar{x_{3}} = … = \bar{x_{n}}\))
\(H_{a}\): ค่าเฉลี่ยของกลุ่มใดกลุ่มหนึ่งต่างจากกลุ่มอื่น

การวิเคราะห์ ANOVA นั้นมีหลายแบบ

One-way ANOVA เป็นการหาความแตกต่างของ 1 ตัวแปร
Two-way ANOVA เป็นการหาความแตกต่างของ 2 ตัวแปร
MANOVA เป็นการหาความแตกต่างที่มากกว่า 2 ตัวแปร
Nested ANOVA เป็นการหาความแตกต่างที่ใน 1 ตัวแปรนั้น มีตัวแปรย่อยอีก

ณ ที่นี้จะกล่าวถึงแค่ one ANOVA ซึ่งมีความซับซ้อนน้อย และนิยมใช้มากที่สุด โดยหลักการโดยง่ายของ ANOVA คือ การเปรียบเทียบความต่างของ ค่าเฉลี่ยทั้งกลุ่ม (Global mean) เปรียบเทียบกับ ผลรวมของค่าเฉลี่ยแต่ละกลุ่ม (Between group mean)

การวิเคราะห์ทางสถิติของ ANOVA นั้นใช้ \(F\)-test ซึ่งเป็นการเปรียบเทียบระหว่าง ความแปรปรวนที่อธิบายได้ และความแปรปรวนที่อธิบายไม่ได้

\[F^{*} = \frac{\text{Explained variance}}{\text{Unexplained variance}} = \frac{\text{Between group variance}}{\text{Within groups variance}}\]

Between group variance คือ ความแปรปรวนของค่าเฉลี่ยแต่ละกลุ่มกับค่าเฉลี่ยทั้งหมด
Within group variance คือ ความแปรปรวนของข้อมูลในกลุ่มนั้น ซึ่งไม่สามารถอธิบายได้ภายใต้สมมติฐานงานวิจัยนั้น

อธิบายโดยใช้ตัวอย่าง iris ในที่นี้เราจะเปรียบเทียบตวามต่างของ Sepal.Width ในแต่ละ Species

aov(Sepal.Width ~ Species, data = iris) |> summary()

##              Df Sum Sq Mean Sq F value Pr(>F)    
## Species       2  11.35   5.672   49.16 <2e-16 ***
## Residuals   147  16.96   0.115                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

อธิบายด้วยภาพ

library(granova)
granova.1w(iris$Sepal.Width, group = iris$Species)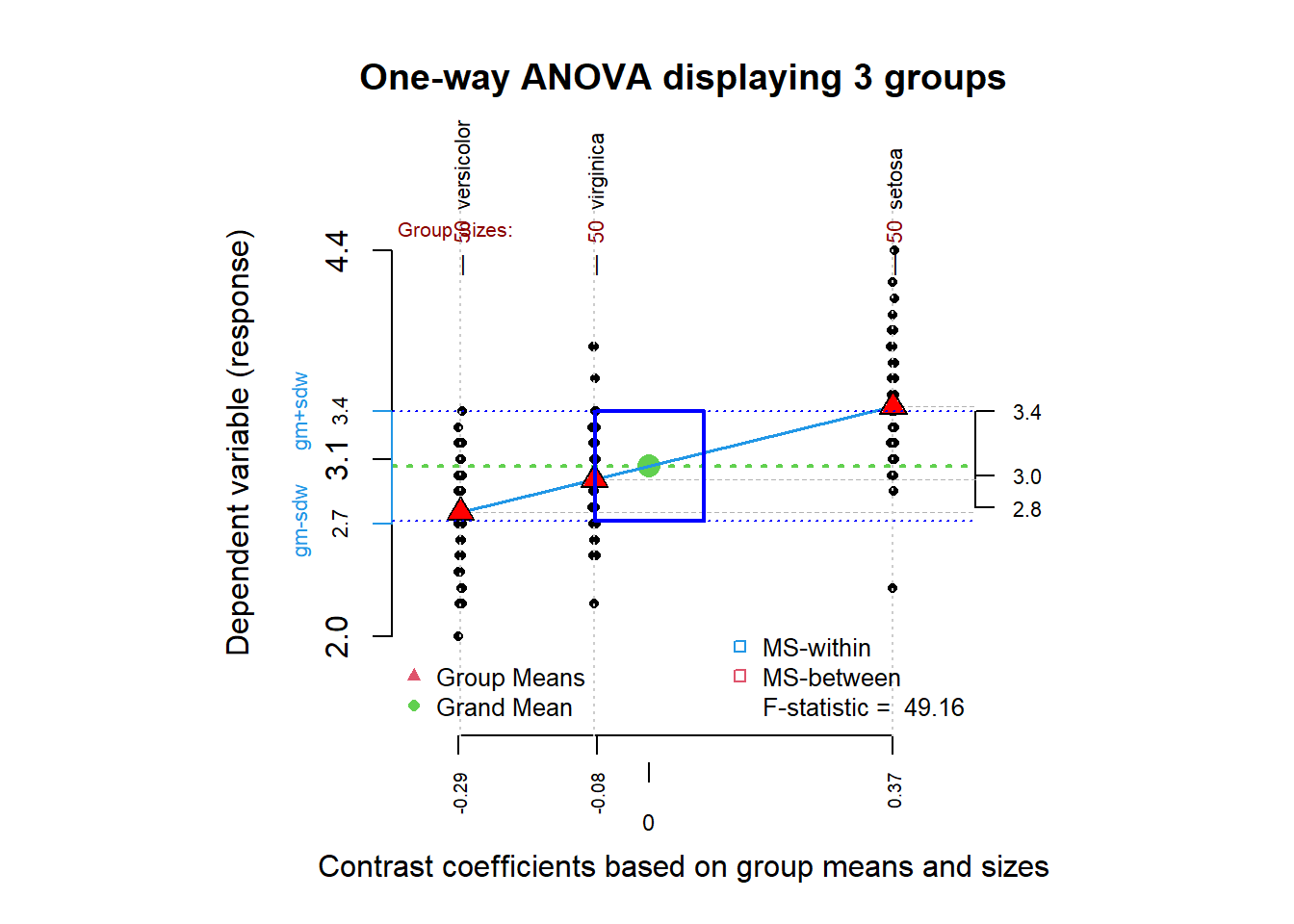

## $grandsum
##     Grandmean        df.bet       df.with        MS.bet       MS.with        F.stat        F.prob 
##          3.06          2.00        147.00          5.67          0.12         49.16          0.00 
## SS.bet/SS.tot 
##          0.40 
## 
## $stats
##            Size Contrast Coef Wt'd Mean Mean Trim'd Mean Var. St. Dev.
## versicolor   50         -0.29      2.77 2.77        2.80 0.10     0.31
## virginica    50         -0.08      2.97 2.97        2.96 0.10     0.32
## setosa       50          0.37      3.43 3.43        3.41 0.14     0.38

รูปสามเหลี่ยม คือ ค่าเฉลี่ยของ Petal.Width ในดอกไม้แต่ละ Species
จุดสีดำ คือ ค่า Petal.Width ในดอกไม้แต่ละดอก
จุดสีเขียว คือ Global mean (Grand mean) คือ ค่าเฉลี่ย Petal.Width เมื่อรวมดอกไม้ทุก Species

จุดประสงค์ของ F-test คือการเปรียบเทียบอัตราส่วนระหว่าง ความแปรปรวนของค่าเฉลี่ยแต่ละกลุ่มกับค่าเฉลี่ยทั้งหมด (mean ของความต่างจุดเขียวกับสามเหลี่ยม) ใกล้กันกับความแปรปรวนของข้อมูลในกลุ่มนั้น (mean ของความต่างระหว่างจุดดำกับกับสามเหลี่ยม) หรือไม่ (ratio ~ 1) ซึ่งค่า \(F\) นั้นจะถูกนำไปคิด \(p\)-value จาก \(F\)-distribution (หลักการเดียวกันกับ \(t\)-test)

สังเกตว่า ท่านไม่สามารถบอกได้ว่ากลุ่มไหนเป็นกลุ่มที่มีค่าเฉลี่ยที่แตกต่างจากทั้งกลุ่ม การที่จะทราบนั้นต้องทำ t.test เปรียบเทียบกันในแต่ละกลุ่ม \(3\choose2\) = 3 ครั้ง การค้นหากลุ่มที่มีความต่างหลัง ANOVA นี้ เรียกว่า Post-hoc test

pairwise.t.test(iris$Sepal.Width, iris$Species)

## 
##  Pairwise comparisons using t tests with pooled SD 
## 
## data:  iris$Sepal.Width and iris$Species 
## 
##            setosa  versicolor
## versicolor < 2e-16 -         
## virginica  9.1e-10 0.0031    
## 
## P value adjustment method: holm

\(p\)-value < 0.05 ทุกกลุ่ม หมายความว่า ทุกกลุ่มมีค่าเฉลี่ยของ Petal.Width ที่แตกต่างกัน

10.3 Correlation test

10.3.1 Pearson correlation

เป็นการทดสอบความสัมพันธ์เชิงเส้นของตัวแปรสองตัวแปร

\[ r_{xy} =\frac{cov(x,y)}{s(x) s(y)} \]

\[ cov(x,y) = \frac{\sum^{n}_{i=1}(x_{i}-\bar{x})(y_{i}-\bar{y})}{n-1} \]

\[ \therefore r_{xy} = \frac{\sum^{n}_{i=1}(x_{i}-\bar{x})(y_{i}-\bar{y})}{\sqrt{\sum^{n}_{i=1}(x_{i}-\bar{x})^{2}}\sqrt{\sum^{n}_{i=1}(y_{i}-\bar{y})^{2}}} \]

ggplot(iris, aes(x = Sepal.Length, y = Petal.Length)) + 
  geom_point(aes(col = Species)) +
  geom_smooth(method = "lm", se = FALSE) +
  theme_bw()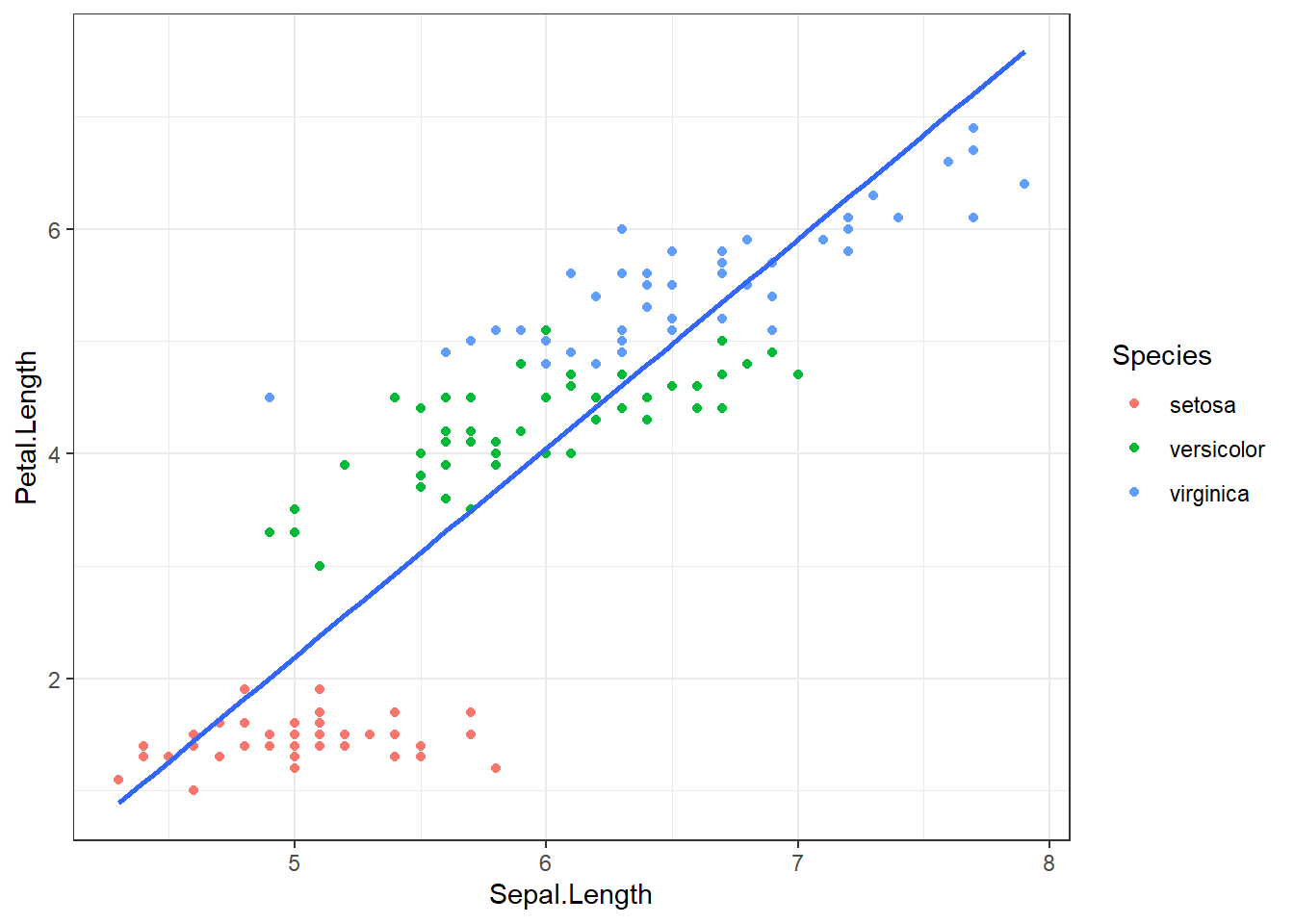

cor(iris$Sepal.Length, iris$Petal.Length)

## [1] 0.8717538

การแปลผลของ Correlation ขึ้นอยู่กับ

ระดับของความสัมพันธ์ = 0-1 ยิ่งเข้าใกล้ 1 ยิ่งสัมพันธ์กันมาก
ทิศทางของความสัมพันธ์ = + ไปทิศทางเดียวกัน - ไปทิศทางตรงข้ามกัน

ท่านสามารถสร้างตาราง Correlation และ \(p\)-value ได้ด้วย Package corrplot

library(corrplot)

iris_cor <- cor(iris[1:4])
iris_cor

##              Sepal.Length Sepal.Width Petal.Length Petal.Width
## Sepal.Length    1.0000000  -0.1175698    0.8717538   0.8179411
## Sepal.Width    -0.1175698   1.0000000   -0.4284401  -0.3661259
## Petal.Length    0.8717538  -0.4284401    1.0000000   0.9628654
## Petal.Width     0.8179411  -0.3661259    0.9628654   1.0000000

iris_cor_p <- cor.mtest(iris[1:4])
iris_cor_p

## $p
##              Sepal.Length  Sepal.Width Petal.Length  Petal.Width
## Sepal.Length 0.000000e+00 1.518983e-01 1.038667e-47 2.325498e-37
## Sepal.Width  1.518983e-01 0.000000e+00 4.513314e-08 4.073229e-06
## Petal.Length 1.038667e-47 4.513314e-08 0.000000e+00 4.675004e-86
## Petal.Width  2.325498e-37 4.073229e-06 4.675004e-86 0.000000e+00
## 
## $lowCI
##              Sepal.Length Sepal.Width Petal.Length Petal.Width
## Sepal.Length    1.0000000  -0.2726932    0.8270363   0.7568971
## Sepal.Width    -0.2726932   1.0000000   -0.5508771  -0.4972130
## Petal.Length    0.8270363  -0.5508771    1.0000000   0.9490525
## Petal.Width     0.7568971  -0.4972130    0.9490525   1.0000000
## 
## $uppCI
##              Sepal.Length Sepal.Width Petal.Length Petal.Width
## Sepal.Length   1.00000000  0.04351158    0.9055080   0.8648361
## Sepal.Width    0.04351158  1.00000000   -0.2879499  -0.2186966
## Petal.Length   0.90550805 -0.28794993    1.0000000   0.9729853
## Petal.Width    0.86483606 -0.21869663    0.9729853   1.0000000

corrplot(iris_cor, method = "shade",type = "upper",order = "AOE", 
         p.mat = iris_cor_p$p, insig = "p-value")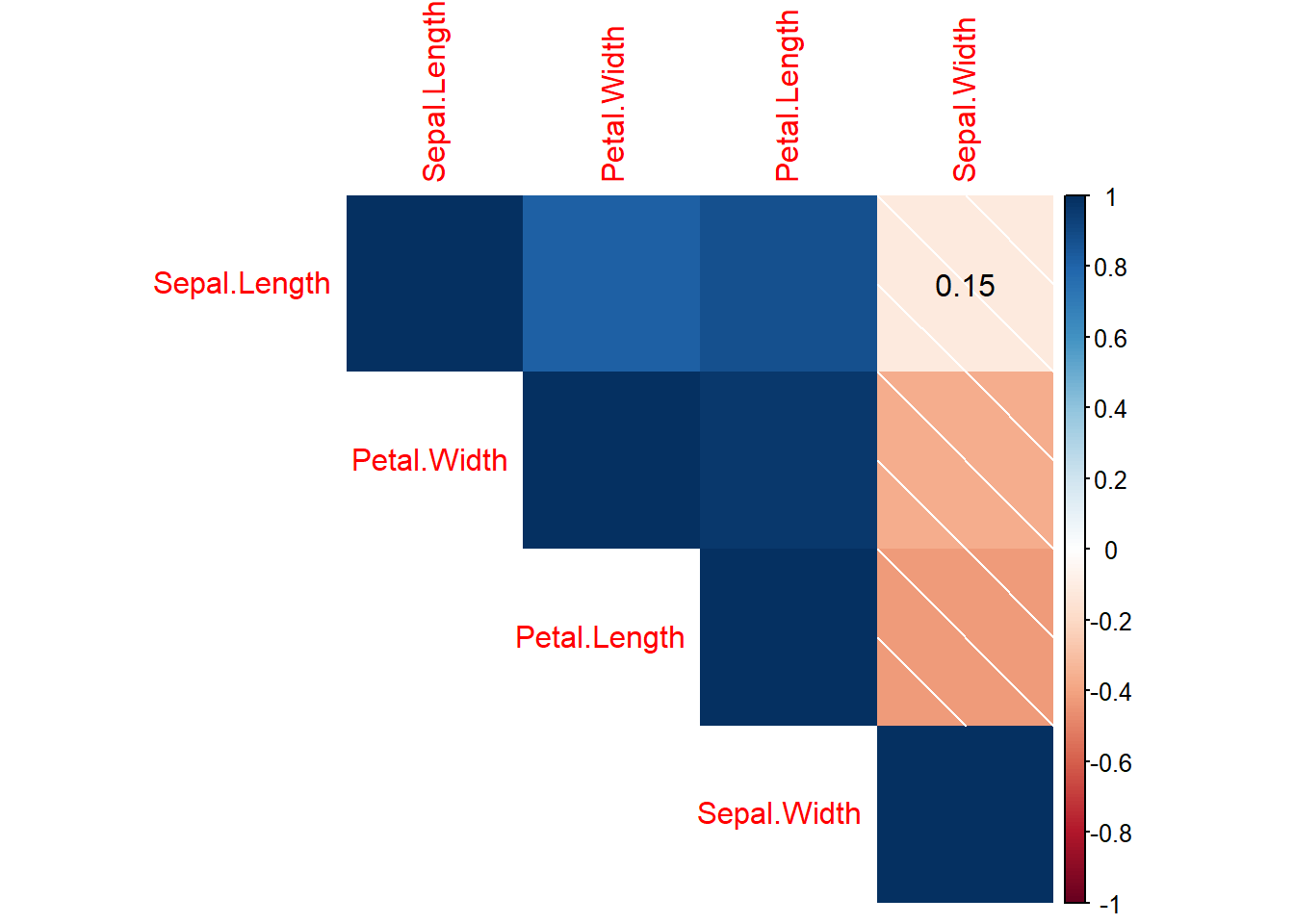

ข้อควรระวัง \(p\)-value ของ Correlation test นั้นอยู่ภายใต้สมมติฐาน (\(t\)-test/\(F\)-test)

\(H_{0}\): ไม่มีความสัมพันธ์เชิงเส้นของทั้งสองตัวแปร (\(r_{xy} = 0\))
\(H_{0}\): มีความสัมพันธ์เชิงเส้นของทั้งสองตัวแปร (\(r_{xy} \neq 0\))

ซึ่งถ้า \(p\) < 0.05 หมายความว่า ท่านมีความมั่นใจมากเพียงพอว่า ความสัมพันธ์เชิงเส้นของทั้งสองตัวแปรนั้น มีมากกว่าการวาดเส้นจากการสร้างจุดแบบสุ่ม ท่านยังคงต้องแปรผลร่วมกับค่า Correlation coefficient ต่อไป

เช่น

\(r_{x,y}\) = 0.2, \(p\) < 0.05 มั่นใจว่ามีความสัมพันธ์เชิงเส้นของสองตัวแปร ความสัมพันธ์เป็นไปในทิศทางเดียวกัน แต่ความสัมพันธ์เชิงเส้นอยู่ในระดับน้อย
\(r_{x,y}\) = 1, \(p\) = 1 ความสัมพันธ์เชิงเส้นอยู่ในระดับดีเยี่ยม แต่ไม่มั่นใจว่ามีความสัมพันธ์กันจริงหรือไม่ เนื่องจากข้อมูลน้อย (เช่น มีข้อมูลเพียงสองจุด \(r_{x,y}\) ย่อมเท่ากับ 1)
\(r_{x,y}\) = 0.3, \(p\) = 1 ความสัมพันธ์เชิงเส้นอยู่ในระดับน้อย แต่ไม่มั่นใจว่ามีความสัมพันธ์กันจริงหรือไม่ เนื่องจากข้อมูลน้อยเกินไป ควรเก็บข้อมูลเพิ่ม
\(r_{x,y}\) = -1, \(p\) < 0.05 มั่นใจว่ามีความสัมพันธ์เชิงเส้นของสองตัวแปร ความสัมพันธ์เป็นไปในทิศทางตรงข้าม และความสัมพันธ์เชิงเส้นอยู่ในระดับดีเยี่ยม

นั่นหมายความว่า ยิ่งจำนวนตัวอย่างเพิ่มขึ้น ความมั่นใจยิ่งเพิ่มขึ้น ไม่ใช่ความสัมพันธ์เพิ่มขึ้น

9 Hypothesis testing

11 Non-parametric test