17 Limma
17.1 Principle
Limma (Linear Model for Microarray Data) (G. Smyth et al., 2023) เป็นหนึ่งใน bioconductor package ที่นิยมใช้อย่างแพร่หลายในการศึกษา ความแตกต่างของการแสดงออกของยีนระหว่างกลุ่มสองกลุ่ม (Differential gene expression; DGE) ในงานทดลอง Microarray
หลักการสำคัญของ limma คือการใช้สมการถดถอยเชิงเส้นในการหา DGE โดยมีสมมติฐานเบื้องต้นว่าค่าความเข้มพื้นหลังที่อ่านได้จาก Probe ของ Microarray นั้นมีการกระจายตัวแบบ Normal distribution ซึ่งหลักการนี้สามารถนำไปปรับใช้ในการหา Differential expression ในงานประเภทอื่นๆ ได้ด้วย เช่น RNA-seq, Proteomics
\(H_{0}\): ไม่มีความแตกต่างกันในการแสดงออกของยีน
\(H_{a}\): มีความแตกต่างกันในการแสดงออกของยีน
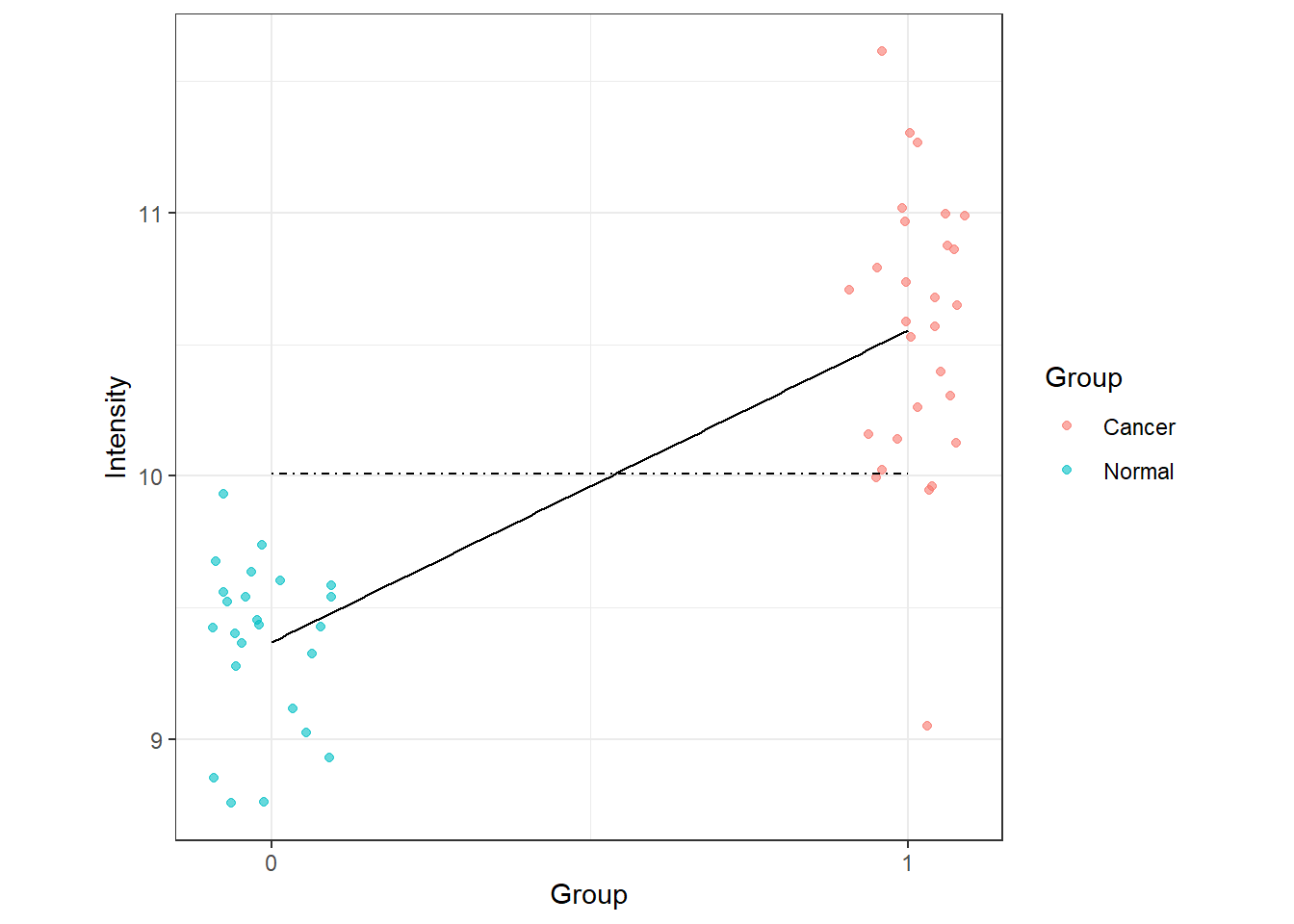
จากกราฟ เส้นประคือเส้นของ \(H_{0}\) หมายถึงการแสดงออกของยีนทั้งหมดสามารถหาได้โดยใช้ค่าเฉลี่ยโดยรวมของทั้งสองกลุ่ม \(\text{Intensity} = \theta_{0} + \epsilon\) และ เส้นทึบคือเส้นของ \(H_{a}\) หมายคือเส้นสมการถดถอยที่ลากผ่านค่าเฉลี่ยของแต่ละกลุ่ม \(\text{Intensity }= \theta_{0} + \theta_{1}*\text{Group} + \epsilon\) ซึ่งทั้งหมดนี้ ก็คือเส้นสมการถดถอยเชิงเส้นตามปกติโดยทั่วไปนั่นเอง โดย limma ซึ่งความแตกต่างตามสมมติฐานนั้น จะถูกทดสอบ โดย \(t\)-test (\(F\)-test ถ้ามากกว่าสองกลุ่ม)
คำถามคือ วิธีการของ limma แตกต่างอย่างไรกับการสร้างสมการถดถอยโดยทั่วไป? เนื่องจากงานประเภท Bioinformatics นั้นมักมีค่าใช้จ่ายในแต่ละการทดลองสูง จำนวนตัวอย่างที่นำมาใช้ในการทดลองนั้นมีไม่มากนัก เช่น 3-4 ตัวอย่างต่อกลุ่ม
\[ t = \frac{\theta_{1}-0}{SE} = \frac{\theta_{1}}{S/\sqrt{n}} \]
ซึ่งเมื่อพิจารณาจากสูตรแล้ว จะเห็นว่าจำนวนตัวอย่างที่ต่ำ ส่งผลให้ \(SE\) สูง มีค่า \(t\) ที่แกว่ง (ตาม \(S\)) และมี Power ที่ต่ำด้วย เนื่องจากมีกลุ่มตัวอย่างน้อย
ผู้นิพนธ์ limma นั้นได้แก้ปัญหานี้โดยใช้หลักการสถิติแบบ Empirical Bayes ชื่อว่า Moderated \(t\)-test โดยหลักการคือ เนื่องจากหลักการของการอ่านข้อมูลใน Microarray ในแต่ละยีนนั้นเป็นไปโดยพร้อมกัน อัตราส่วนความแปรปรวนของยีนแต่ละตัวที่อ่านค่าได้นั้นจะเท่าๆ กันตลอดทั้ง Array ดังนั้นจึงสามารถยืมข้อมูลของความแปรปรวนมาจากทุกยีนทั้งหมด มาสร้างเป็น ความน่าจะเป็นก่อนหน้า (Prior probability) เพื่อนำมาถ่วงน้ำหนักความเป็นไปได้กับยีนแต่ละตัว เกิดเป็นความน่าจะเป็นภายหลัง (Posterior probability)
cx_nc <- GSE63514 |>
as.data.frame() |>
dplyr::select(contains(c("Normal", "Cancer")))
cx_var <- apply(cx_nc, 1, var)
ggplot(data = NULL, aes(x = cx_var)) +
geom_density(fill = "skyblue") +
scale_x_continuous(breaks = seq(0,3,0.25), limits = c(0,3)) +
annotate("text", x = mean(cx_var)+0.35, y = 4, label= "Mean variance") +
labs(x = "Variance") +
geom_vline(xintercept = mean(cx_var), linetype = "dashed") +
theme_bw() 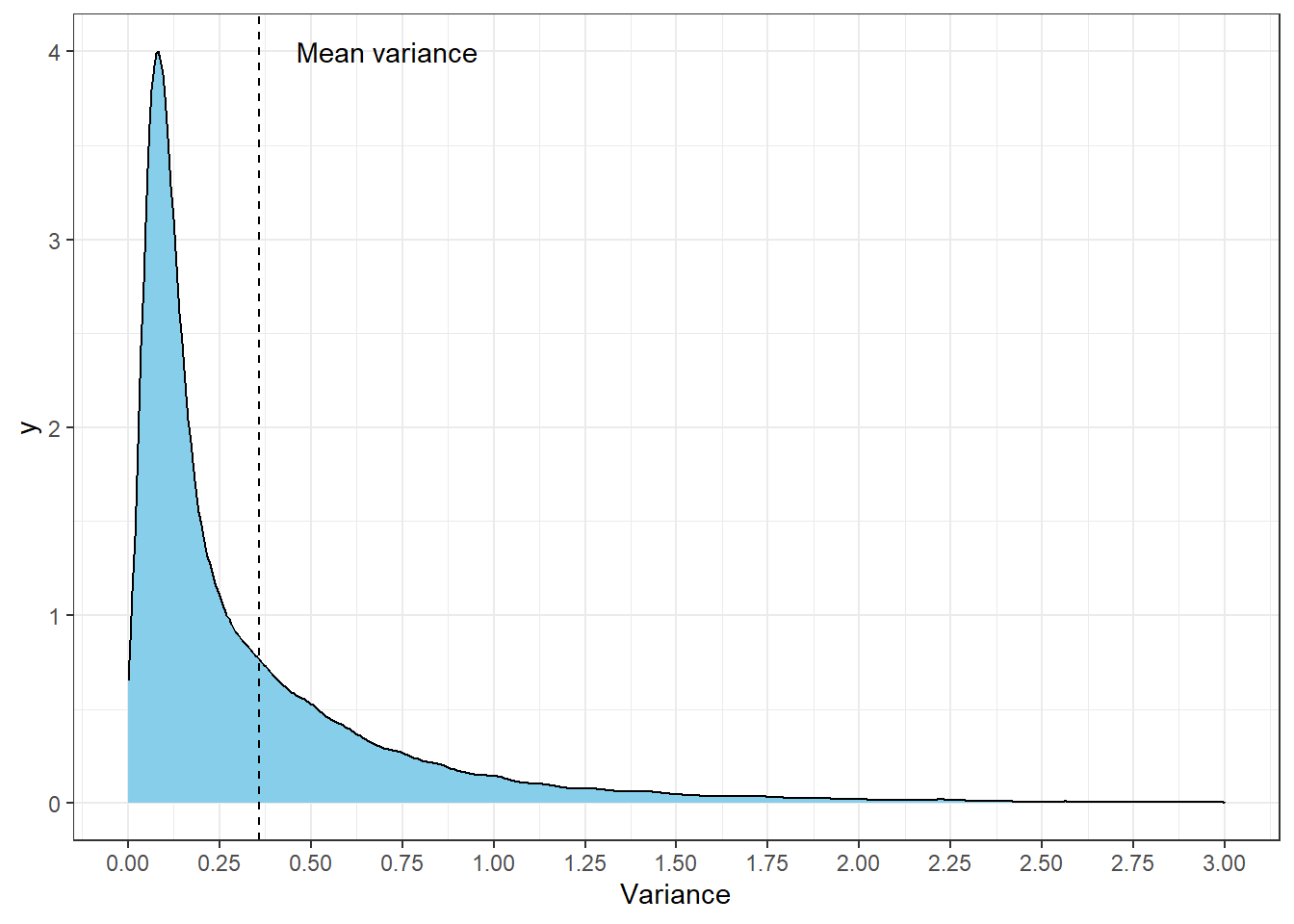
ค่า Mean variance นี้จะถูกนำไปถ่วงน้ำหนักความแปรปรวนเดิมของแต่ละยีน และจะถูกนำไปใช้ในการคำนวณใหม่ เรียกว่า Moderated \(t\) (G. K. Smyth, 2004)
\[ \tilde{t_{gj}} = \sqrt\frac{d_{0} + d_{g}}{d_{g}}\times\frac{\hat{\beta_{gj}}}{\sqrt{s^{2}_{*,g}/n_{gj}}} \]
\[ s^{2}_{*,g} = s^{2}_{g}+(\frac{d_{0}}{d_{g}})s_{0}^{2} \]
สังเกตว่า ค่า \(\tilde{t}\) นั้นจะถูก Moderated ให้เข้าสู่ \(d_{0}\) (Prior degree of freedom) และ \(s_{0}\) (Prior variance) ส่งผลให้
ถ้า \(s_{g}\) > \(s_{0}\): \(s_{*,g}\) จะเพิ่มขึ้นจาก \(s_{g}\) เล็กน้อย ทำให้ \(\tilde{t}\) ลดลงเล็กน้อย เมื่อเทียบกับ \(\tilde{t}\) ที่เพิ่มขึ้นจาก \(\sqrt{\frac{d_{0}+d_{g}}{d_{g}}}\)
ถ้า \(s_{g}\) < \(s_{0}\): \(s_{*,g}\) จะเพิ่มขึ้นจาก \(s_{g}\) เป็นอย่างมาก ทำให้ \(\tilde{t}\) ลดลงมาก เมื่อเทียบกับ \(\tilde{t}\) ที่เพิ่มขึ้นจาก \(\sqrt{\frac{d_{0}+d_{g}}{d_{g}}}\)
ถ้า \(s_{g}\) = \(s_{0}\): \(s_{*,g}\) การลดลงของ \(\tilde{t}\) จะหักล้างกับการเพิ่มขึ้นของ \(\tilde{t}\) จาก \(\sqrt{\frac{d_{0}+d_{g}}{d_{g}}}\) พอดี
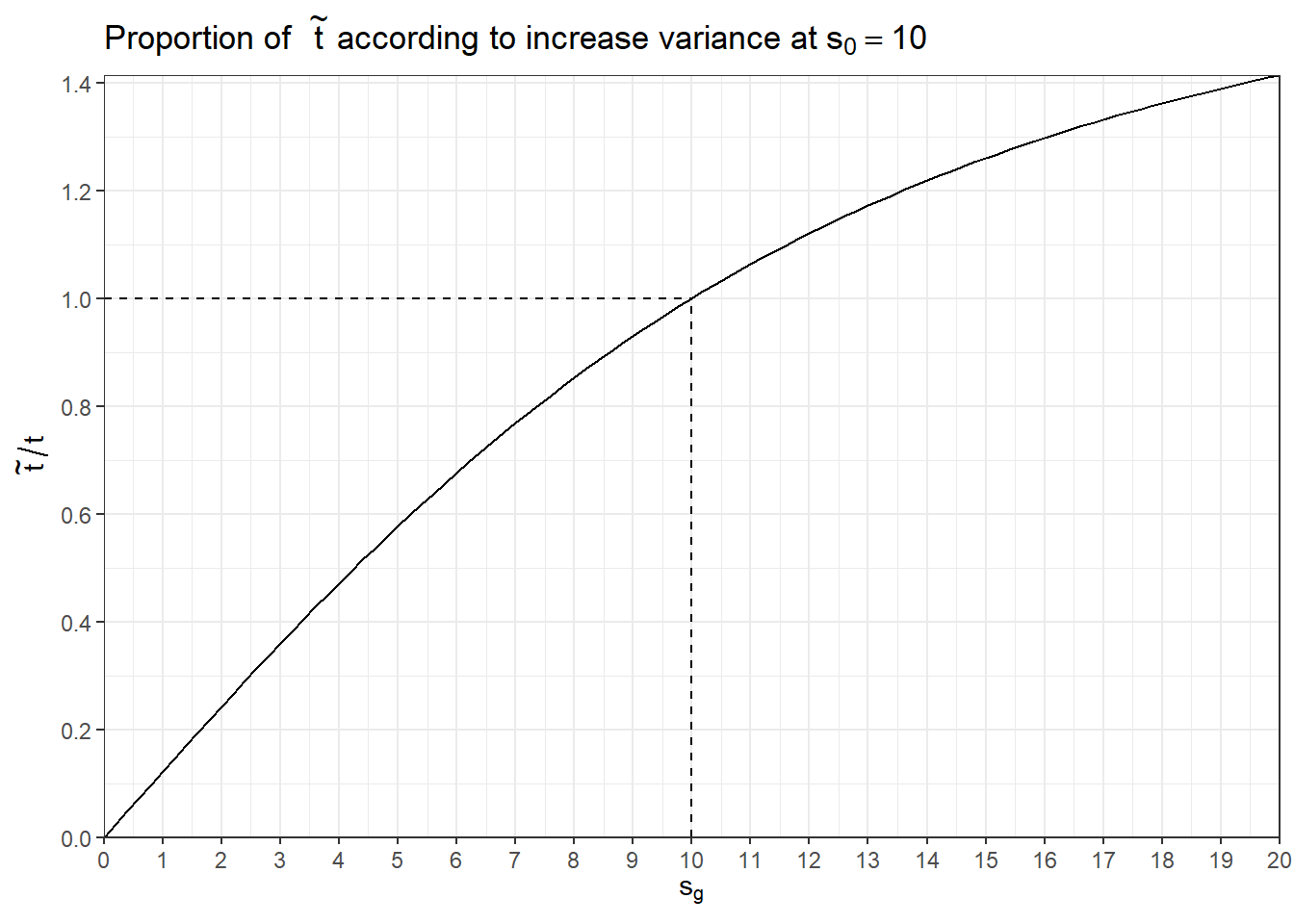
ทั้งหมดนี้จะส่งผลให้ มี Moderate effect ของการคำนวณค่า \(\tilde{t}\) และมี Degree of freedom ที่เพิ่มขึ้นส่งผลให้ Power สูงขึ้น (เพราะการกระจายตัวแคบลง)
17.2 Example
ต่อจากนี้จะยกตัวอย่างการคำนวณ DGE ระหว่างกลุ่มโดยใช้ limma ต่อจาก GSE63514 ซึ่งครั้งนี้จะเทียบทุกกลุ่ม และเทียบทุกยีน
ก่อนอื่นจะต้องสร้างสมการเชิงเส้นของกลุ่มแต่ละกลุ่มขึ้นมาก่อน
pData <- GSE63514_meta |>
select(title) |>
mutate(group = gsub("-\\d+", "", title))
unique(pData$group)## [1] "Normal" "CIN1" "CIN2" "CIN3" "Cancer"
cx_mod <- model.matrix(~ 0 + group, data = pData)
as.data.frame(cx_mod) # Display as dataframeแมทริกซ์ที่เห็นนี้ ข้อมูลของ Sample แต่ละคน โดยแต่ละคอลัมน์จะเป็นตัวแทนของกลุ่มของ Sample นั้น เช่น คนที่ 1 จะมีตัวเลข [0 0 0 0 1] บ่งบอกว่าเป็นชิ้นเนื้อประเภท Cancer และคนสุดท้ายเป็น [1 0 0 0 0] บ่งบอกว่าชิ้นเนื้อประเภท Normal
ต่อจากนั้นเราจะสร้าง contrast matrix ขึ้นมาเพื่อนำไปใช้อ้างอิงในการเทียบ DEG
library(limma)
contrasts <- apply(combn(colnames(cx_mod),2)[2:1,], 2, paste, collapse = "-")
contrasts## [1] "groupCIN1-groupCancer" "groupCIN2-groupCancer" "groupCIN3-groupCancer"
## [4] "groupNormal-groupCancer" "groupCIN2-groupCIN1" "groupCIN3-groupCIN1"
## [7] "groupNormal-groupCIN1" "groupCIN3-groupCIN2" "groupNormal-groupCIN2"
## [10] "groupNormal-groupCIN3"
contrasts.matrix <- makeContrasts(contrasts = contrasts, levels = colnames(cx_mod))
contrasts.matrix## Contrasts
## Levels groupCIN1-groupCancer groupCIN2-groupCancer groupCIN3-groupCancer groupNormal-groupCancer
## groupCancer -1 -1 -1 -1
## groupCIN1 1 0 0 0
## groupCIN2 0 1 0 0
## groupCIN3 0 0 1 0
## groupNormal 0 0 0 1
## Contrasts
## Levels groupCIN2-groupCIN1 groupCIN3-groupCIN1 groupNormal-groupCIN1 groupCIN3-groupCIN2
## groupCancer 0 0 0 0
## groupCIN1 -1 -1 -1 0
## groupCIN2 1 0 0 -1
## groupCIN3 0 1 0 1
## groupNormal 0 0 1 0
## Contrasts
## Levels groupNormal-groupCIN2 groupNormal-groupCIN3
## groupCancer 0 0
## groupCIN1 0 0
## groupCIN2 -1 0
## groupCIN3 0 -1
## groupNormal 1 1สังเกตว่าแต่ละคอลัมน์ผลรวมจะเท่ากับ 0 เนื่องจาก \(H_{0}\) ว่าไม่มีความแตกต่างกันในการแสดงออกของยีน (= 0) นั่นเอง
เมื่อได้ design matrix ต่อไปคือการ fit linear regression ตาม model โดยข้อมูลจะต้องอยู่ในรูปตัวเลขทั้งหมด ดังนั้นจะต้องปรับแต่ง ข้อมูล expression เริ่มต้นเล็กน้อย
GSE63514_fixed <- GSE63514 |>
column_to_rownames("prob")ต่อจากนั้นจะ fit model ด้วย lmFit() และเทียบแต่ละกลุ่มด้วย contrasts.fit()
cx_fit <- lmFit(GSE63514_fixed, design = cx_mod)
cx_fit_contrasts <- contrasts.fit(cx_fit, contrasts.matrix)สุดท้ายเราจะทำการคำนวณ Moderated t-test โดยใช้ eBayes()
cx_fit_contrasts_eB <- eBayes(cx_fit_contrasts)สุดท้ายคือการแสดงผล DGE จากการคำนวณทั้งหมดโดยใช้ topTable() ซึ่งจะแสดง Moderated \(F\)-test (ANOVA) และ \(p\)-value, Adjusted \(p\)-value
topTable(cx_fit_contrasts_eB, n = 100) # First 100 genesและสามารถเรียกดู \(t\)-test แต่ละกลุ่มได้โดยการระบุ coef
topTable(cx_fit_contrasts_eB, coef = 1, n = 100) # เรียงตาม contrasts.matrixโดย logFC คือ Log2 fold-change ของ Gene expression แต่ละตัว
map(1:length(colnames(contrasts.matrix)),
~topTable(cx_fit_contrasts_eB, coef = .x)) |>
set_names(colnames(contrasts.matrix))## $`groupCIN1-groupCancer`
## logFC AveExpr t P.Value adj.P.Val B
## 206025_s_at -1.2599869 6.600127 -7.954562 8.906110e-13 4.869415e-08 18.36296
## 222835_at 2.7037467 11.390512 7.656871 4.369597e-12 9.910994e-08 16.87732
## 232855_at 1.9511837 7.464893 7.581694 6.508984e-12 9.910994e-08 16.50502
## 220090_at 5.1219007 11.675811 7.561290 7.250842e-12 9.910994e-08 16.40418
## 205185_at 3.6701214 12.344023 7.312213 2.685207e-11 2.682614e-07 15.18098
## 235651_at 2.5105300 11.627430 7.294601 2.943884e-11 2.682614e-07 15.09504
## 203857_s_at -1.3379967 8.865472 -7.135465 6.732460e-11 5.258532e-07 14.32218
## 226506_at 2.2236684 10.612391 6.929967 1.938536e-10 1.324868e-06 13.33417
## 207821_s_at -0.8531452 7.215208 -6.723744 5.531008e-10 3.360087e-06 12.35491
## 40016_g_at 1.6956215 11.063432 6.637076 8.558517e-10 4.077549e-06 11.94725
##
## $`groupCIN2-groupCancer`
## logFC AveExpr t P.Value adj.P.Val B
## 206025_s_at -1.380196 6.600127 -10.011010 1.030733e-17 5.635535e-13 29.24779
## 210495_x_at -2.715234 10.074149 -8.851861 6.668495e-15 1.617849e-10 23.13848
## 216442_x_at -2.764813 9.747865 -8.800039 8.877086e-15 1.617849e-10 22.86809
## 205464_at 2.458379 9.030410 8.665389 1.863583e-14 2.435352e-10 22.16703
## 218468_s_at -2.659120 5.349137 -8.625147 2.324822e-14 2.435352e-10 21.95795
## 219597_s_at 1.847612 10.636695 8.599759 2.672540e-14 2.435352e-10 21.82616
## 211719_x_at -2.978875 9.677495 -8.468114 5.497177e-14 3.537199e-10 21.14420
## 227140_at -3.349588 6.795510 -8.460792 5.721706e-14 3.537199e-10 21.10635
## 212464_s_at -2.941674 9.149103 -8.457596 5.822549e-14 3.537199e-10 21.08983
## 220090_at 4.972371 11.675811 8.433644 6.636766e-14 3.628652e-10 20.96605
##
## $`groupCIN3-groupCancer`
## logFC AveExpr t P.Value adj.P.Val B
## 206025_s_at -1.3149204 6.600127 -11.027724 3.311442e-20 1.810531e-15 34.44112
## 218468_s_at -2.5804213 5.349137 -9.677614 6.709207e-17 1.834129e-12 27.33557
## 227566_at -1.2024603 6.615340 -8.972807 3.415686e-15 5.539439e-11 23.65417
## 206026_s_at -1.3312089 6.219060 -8.941927 4.052630e-15 5.539439e-11 23.49384
## 219597_s_at 1.6246901 10.636695 8.743700 1.211057e-14 1.324291e-10 22.46704
## 210495_x_at -2.2247812 10.074149 -8.386172 8.599897e-14 7.836656e-10 20.62733
## 205464_at 2.0342073 9.030410 8.290557 1.447645e-13 1.130714e-09 20.13838
## 216442_x_at -2.2269918 9.747865 -8.195711 2.422825e-13 1.655849e-09 19.65479
## 212464_s_at -2.4481475 9.149103 -8.138402 3.304613e-13 1.950668e-09 19.36330
## 213434_at -0.7553377 8.747262 -8.124238 3.567751e-13 1.950668e-09 19.29135
##
## $`groupNormal-groupCancer`
## logFC AveExpr t P.Value adj.P.Val B
## 232855_at 2.353804 7.464893 10.762249 1.485735e-19 8.123254e-15 33.65727
## 206025_s_at -1.407391 6.600127 -10.455133 8.425180e-19 2.303233e-14 31.99032
## 207802_at 6.508949 7.727577 10.008609 1.044759e-17 1.904073e-13 29.57022
## 205464_at 2.730049 9.030410 9.855695 2.468951e-17 2.847392e-13 28.74320
## 212621_at -1.668245 9.041825 -9.816828 3.071485e-17 2.847392e-13 28.53318
## 226506_at 2.672522 10.612391 9.800471 3.367040e-17 2.847392e-13 28.44482
## 210262_at 3.001186 6.730272 9.786321 3.645495e-17 2.847392e-13 28.36840
## 214431_at -1.402298 10.718458 -9.638181 8.369057e-17 5.086653e-13 27.56901
## 202055_at -1.184061 9.912045 -9.638095 8.373092e-17 5.086653e-13 27.56855
## 222835_at 2.873757 11.390512 9.576350 1.183340e-16 6.469909e-13 27.23578
##
## $`groupCIN2-groupCIN1`
## logFC AveExpr t P.Value adj.P.Val B
## 217575_s_at -0.2603589 4.108856 -4.119514 6.827838e-05 0.9999659 -1.555995
## 219450_at 1.3974047 8.021937 4.108238 7.128229e-05 0.9999659 -1.572421
## 204779_s_at 1.0783374 9.084288 3.979722 1.157851e-04 0.9999659 -1.757629
## 214611_at -0.3799563 5.371863 -3.974482 1.180717e-04 0.9999659 -1.765101
## 219358_s_at -0.5104374 7.798451 -3.972613 1.188977e-04 0.9999659 -1.767765
## 216973_s_at 0.9522317 9.119675 3.794046 2.290469e-04 0.9999659 -2.018449
## 242979_at -1.3010652 7.799901 -3.791582 2.310954e-04 0.9999659 -2.021855
## 228152_s_at -1.1207177 8.651740 -3.777430 2.431998e-04 0.9999659 -2.041386
## 235350_at 1.5458201 7.528341 3.714830 3.043333e-04 0.9999659 -2.127184
## 238175_at -0.3896401 4.538269 -3.696149 3.252317e-04 0.9999659 -2.152598
##
## $`groupCIN3-groupCIN1`
## logFC AveExpr t P.Value adj.P.Val B
## 204603_at 0.7024178 8.164955 5.356714 3.887100e-07 0.01455424 5.999781
## 204775_at 0.6352418 7.355724 5.222561 7.081541e-07 0.01455424 5.472794
## 202954_at 0.8500242 10.181699 5.147294 9.876396e-07 0.01455424 5.180686
## 209054_s_at 0.7012696 9.439562 5.130188 1.064782e-06 0.01455424 5.114663
## 225784_s_at -0.5082652 7.521747 -5.022461 1.703992e-06 0.01765170 4.702034
## 226308_at 0.8984545 7.797713 4.964062 2.193210e-06 0.01765170 4.480667
## 209053_s_at 0.7712176 8.902046 4.936377 2.470436e-06 0.01765170 4.376302
## 219490_s_at 0.5818629 8.117920 4.926008 2.582782e-06 0.01765170 4.337314
## 202183_s_at 0.8829252 8.037612 4.885240 3.074616e-06 0.01867829 4.184526
## 226456_at 1.0098740 10.334927 4.802377 4.369883e-06 0.02274771 3.876535
##
## $`groupNormal-groupCIN1`
## logFC AveExpr t P.Value adj.P.Val B
## 210262_at 1.8942513 6.730272 5.109272 1.167105e-06 0.06381149 0.1414762
## 226702_at -1.8232496 9.133420 -4.447203 1.888683e-05 0.51631880 -0.9456764
## 219258_at -0.9936006 8.488497 -4.236185 4.353151e-05 0.59048057 -1.2746881
## 217905_at -0.5415615 8.950872 -4.227458 4.503515e-05 0.59048057 -1.2880906
## 229450_at -1.6129526 9.183332 -4.170784 5.608285e-05 0.59048057 -1.3747156
## 209969_s_at -1.4138293 10.354201 -4.133184 6.479897e-05 0.59048057 -1.4317897
## 204510_at -1.0598884 9.627055 -4.069143 8.270786e-05 0.64600748 -1.5282574
## 227609_at -1.1735956 9.637705 -4.001474 1.067367e-04 0.70559370 -1.6291527
## 210766_s_at -0.6423773 11.534705 -3.978886 1.161471e-04 0.70559370 -1.6625908
## 204994_at -1.1295418 10.139366 -3.914339 1.475994e-04 0.80699981 -1.7574641
##
## $`groupCIN3-groupCIN2`
## logFC AveExpr t P.Value adj.P.Val B
## 31845_at 0.5943656 9.673283 4.745089 5.560039e-06 0.1145089 1.57530720
## 214858_at -0.8133322 5.396801 -4.732526 5.860234e-06 0.1145089 1.54352542
## 232222_at 0.3363060 6.001814 4.715848 6.283067e-06 0.1145089 1.50141268
## 241014_at -1.1644315 6.254372 -4.243388 4.232694e-05 0.5785564 0.34663636
## 205968_at 0.8210918 9.169976 4.159667 5.853537e-05 0.6236596 0.15019705
## 220040_x_at -0.3462818 7.659149 -4.061818 8.503499e-05 0.6236596 -0.07605645
## 229782_at -0.7239349 6.901729 -3.981172 1.151596e-04 0.6236596 -0.25975588
## 1563881_at -0.7137692 4.397457 -3.971422 1.194271e-04 0.6236596 -0.28179416
## 200060_s_at 0.3245884 11.538188 3.970706 1.197462e-04 0.6236596 -0.28341066
## 236010_at -0.5131600 5.533651 -3.936483 1.359910e-04 0.6236596 -0.36045186
##
## $`groupNormal-groupCIN2`
## logFC AveExpr t P.Value adj.P.Val B
## 223556_at -1.445308 9.156569 -7.093800 8.350796e-11 4.565797e-06 13.83546
## 235609_at -1.432506 9.066440 -6.867548 2.666254e-10 7.288873e-06 12.78063
## 201930_at -1.280896 11.792626 -6.667073 7.360367e-10 1.262858e-05 11.85781
## 218039_at -1.450594 11.879667 -6.597757 1.042446e-09 1.262858e-05 11.54149
## 218585_s_at -1.642935 10.431612 -6.577297 1.154877e-09 1.262858e-05 11.44841
## 205909_at -1.310771 9.479550 -6.532028 1.447888e-09 1.319388e-05 11.24291
## 225655_at -1.473806 10.563237 -6.484394 1.835405e-09 1.366560e-05 11.02737
## 226456_at -1.292656 10.334927 -6.467152 1.999539e-09 1.366560e-05 10.94953
## 204026_s_at -1.136500 11.876375 -6.437869 2.312056e-09 1.404574e-05 10.81756
## 228273_at -1.497697 9.925345 -6.403594 2.739372e-09 1.497751e-05 10.66344
##
## $`groupNormal-groupCIN3`
## logFC AveExpr t P.Value adj.P.Val B
## 218585_s_at -2.1455228 10.431612 -9.819011 3.034047e-17 9.812847e-13 28.38863
## 204510_at -1.9576326 9.627055 -9.789077 3.589519e-17 9.812847e-13 28.22861
## 221521_s_at -1.7711864 10.294773 -9.687331 6.353396e-17 1.157906e-12 27.68508
## 222680_s_at -1.8101779 8.533391 -9.265312 6.725115e-16 6.884628e-12 25.43791
## 225655_at -1.8399722 10.563237 -9.254393 7.146915e-16 6.884628e-12 25.37995
## 226456_at -1.6163749 10.334927 -9.244420 7.555147e-16 6.884628e-12 25.32702
## 235609_at -1.6711061 9.066440 -9.158340 1.219785e-15 9.527392e-12 24.87058
## 205339_at -1.8494642 9.227739 -9.117800 1.528068e-15 1.044339e-11 24.65586
## 204603_at -0.9813232 8.164955 -9.000435 2.930854e-15 1.649719e-11 24.03517
## 218039_at -1.7300249 11.879667 -8.995189 3.017319e-15 1.649719e-11 24.00746ท่านสามารถสรุปข้อมูล DGE ได้โดยใช้ decideTests()
results <- decideTests(cx_fit_contrasts_eB, fc=log2(1.5))
summary(results)## groupCIN1-groupCancer groupCIN2-groupCancer groupCIN3-groupCancer groupNormal-groupCancer
## Down 2221 3818 2402 6317
## NotSig 50408 47570 50026 40811
## Up 2046 3287 2247 7547
## groupCIN2-groupCIN1 groupCIN3-groupCIN1 groupNormal-groupCIN1 groupCIN3-groupCIN2
## Down 0 34 0 0
## NotSig 54675 54548 54675 54675
## Up 0 93 0 0
## groupNormal-groupCIN2 groupNormal-groupCIN3
## Down 311 2214
## NotSig 54333 50612
## Up 31 1849
vennDiagram(results[,1:5]) # max 5 groups
17.3 Mean-variance relationship
ในบางข้อมูลนั้นมีความสัมพันธ์ระหว่างค่าเฉลี่ยและความแปรปรวน ซึ่งสามารถตรวจสอบได้โดยใช้ plotSA()
plotSA(cx_fit_contrasts_eB) 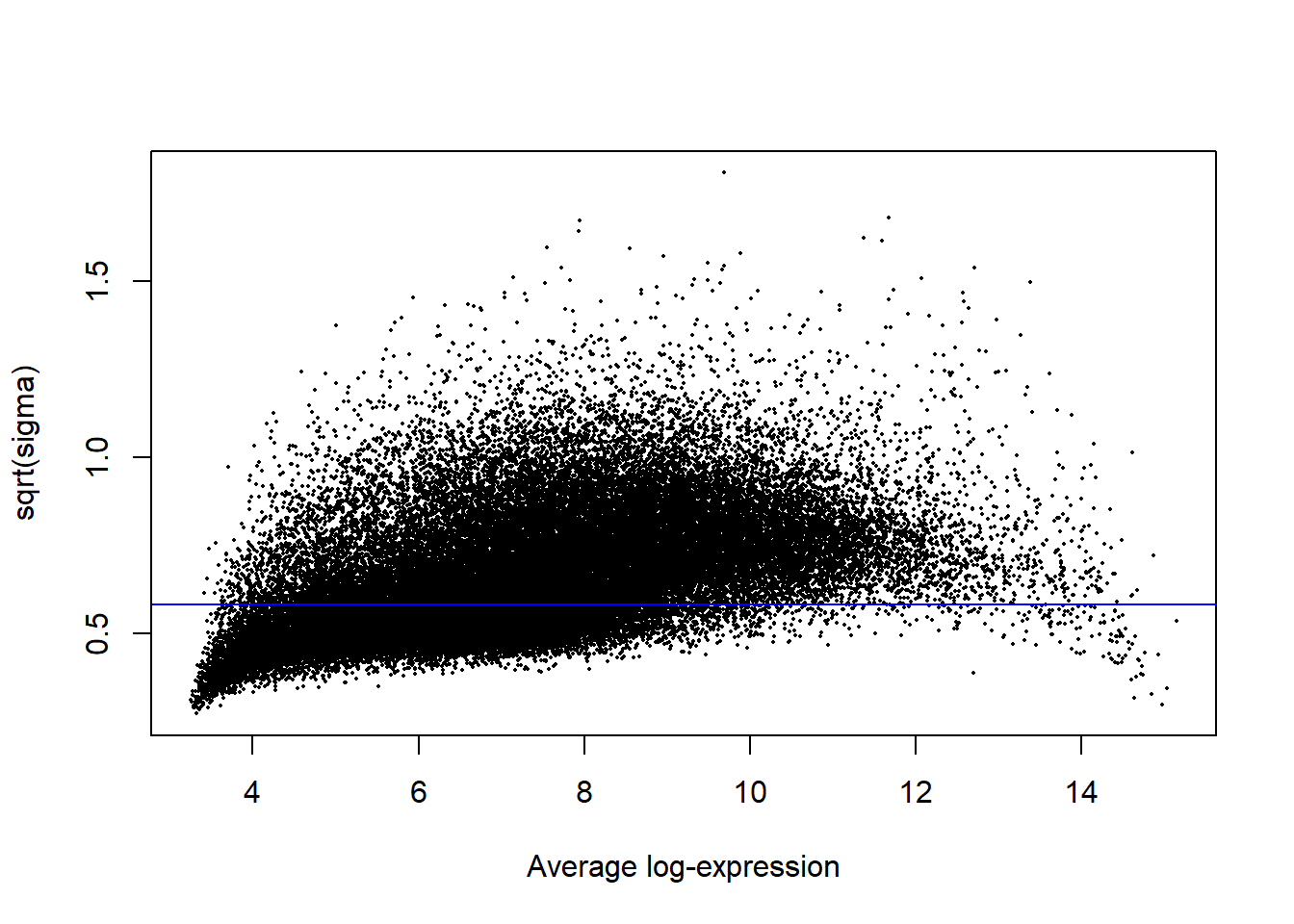
จากกราฟจะพบความสัมพันธ์ระหว่าง Average log-expression และ sqrt(sigma) แปลว่ามีความสัมพันธ์ระหว่างค่าเฉลี่ยและความแปรปรวน เนื่องจาก Linear model นั้นมีสมมติฐานว่า ความแปรปรวนนั้นคงที่ตลอด (Homoscedasticity) การสร้างสมการแบบธรรมดาอาจจะทำให้เกิด False positive มากกว่าปกติ ซึ่ง limma นั้นมีฟังก์ชันที่ปรับสมการตามแนวโน้มของความแปรปรวนด้วย eBayes(..., trend = TRUE)
cx_fit_contrasts_eB_trend <- eBayes(cx_fit_contrasts, trend = TRUE)
results_trend <- decideTests(cx_fit_contrasts_eB, fc = log2(1.5))
summary(results_trend)## groupCIN1-groupCancer groupCIN2-groupCancer groupCIN3-groupCancer groupNormal-groupCancer
## Down 2221 3818 2402 6317
## NotSig 50408 47570 50026 40811
## Up 2046 3287 2247 7547
## groupCIN2-groupCIN1 groupCIN3-groupCIN1 groupNormal-groupCIN1 groupCIN3-groupCIN2
## Down 0 34 0 0
## NotSig 54675 54548 54675 54675
## Up 0 93 0 0
## groupNormal-groupCIN2 groupNormal-groupCIN3
## Down 311 2214
## NotSig 54333 50612
## Up 31 1849เมื่อทำการพล็อตความสัมพันธ์ระหว่างค่าเฉลี่ยและความแปรปรวนอีกครั้ง จะพบว่าโมเดลนั้นถูกปรับตามความแปรปรวนแล้ว
plotSA(cx_fit_contrasts_eB_trend)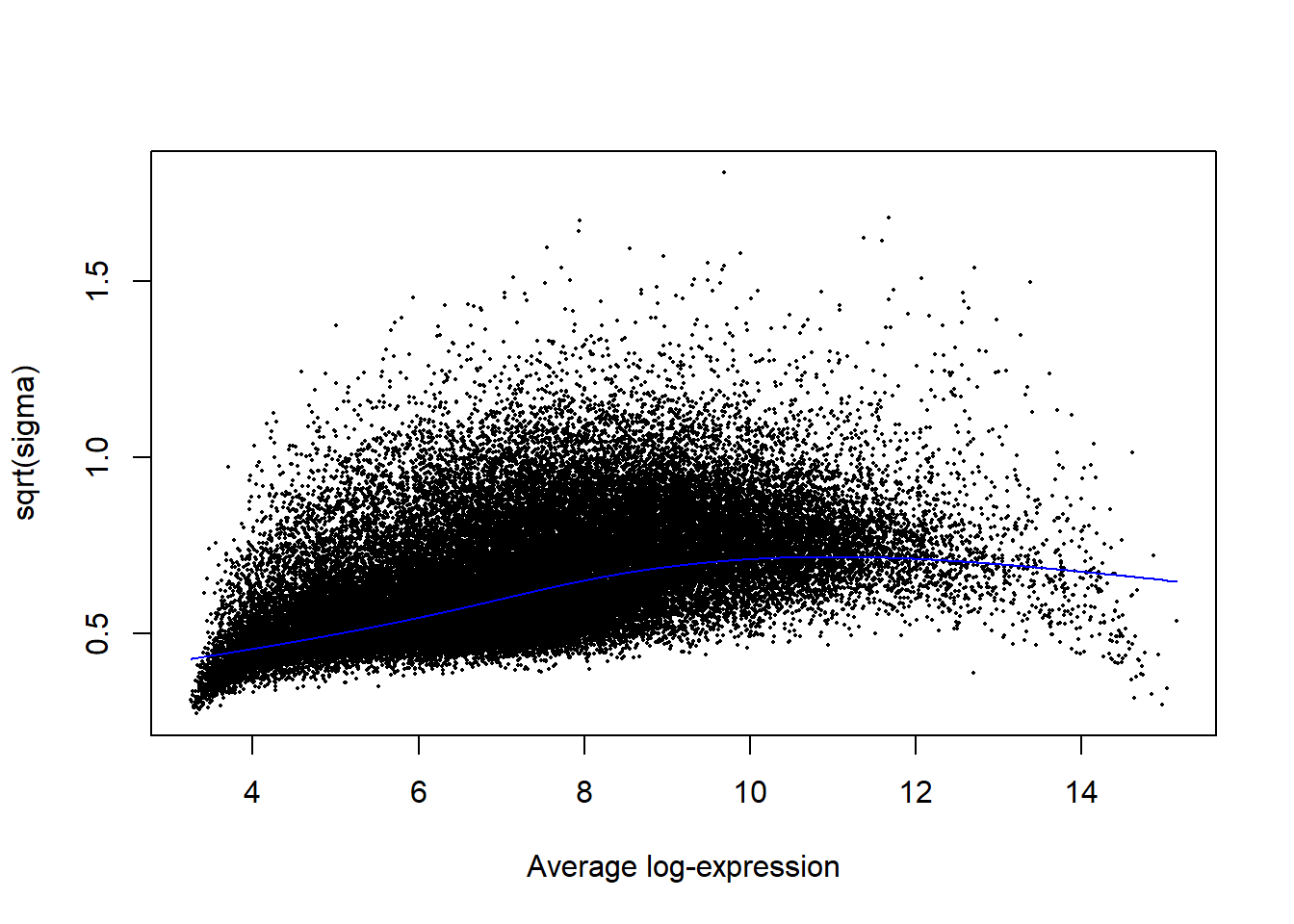
การใช้ trend = TRUE นี้มีความสำคัญมากในการประยุกต์ใช้ limma ในการวิเคราะห์ข้อมูลแบบอื่นๆ ที่ไม่ใช่ Microarray เช่น RNA-seq, Proteomics เนื่องจากข้อมูลมักจะมีความสัมพันธ์ระหว่างค่าเฉลี่ยกับตัวแปรสูง (Heteroscedasticity)